algorithm

Bcrypt是单向Hash加密算法，类似Pbkdf2算法 不可反向破解生成明文。

https://zhuanlan.zhihu.com/p/370775073

基数树是一种比较节省空间的树结构，下图展示了基数树的结构，其中key是树的构建方式，在这里，key是一个32位的整数，为了避免层数过深，所以使用两位代表子节点的索引，基数树就是依据二进制串来生成树结构。值value被储存在叶节点。 https://zhuanlan.zhihu.com/p/95814705 http://www.360doc.com/content/19/0305/18/496343_819431105.shtml

https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html

LZ77、LZ78、霍夫曼编码、滑动窗口、Rabin-Karp算法、哈希链、I/O缓冲区

递归是非常常见的一种算法，由于代码简洁而应用广泛，但递归相比顺序执行或循环程序，时间复杂度难以计算，而master公式就是用于计算递归程序的时间复杂度。

并查集一般解决的是对于给定的多个集合之间的合并和查询问题，假设我们现在有n个集合，每个集合都有一个独立的编号，我们对这些初始集合进行n次合并操作（每次将两个集合合并成一个），然后进行m次询问，查找两个元素是否在同一个集合之中。

Go 工程时，总会遇到 2 个经典问题，特别的折腾人。

1. ASCII码

彩虹表（Rainbow Table）是一种主流的密码破解技术，它事先把所有可能的密码计算出哈希并保存在索引文件中，在需要破解时只需根据哈希对索引文件进行查询即可很快获得明文密码，在避免大量的重复计算的同时，也大大提高了密码的破解速度。

Knuth-Morris-Pratt 字符串查找算法，简称为 KMP算法，常用于在一个文本串 S 内查找一个模式串 P 的出现位置。 这个算法由 Donald Knuth、Vaughan Pratt、James H. Morris 三人于 1977 年联合发表，故取这 3 人的姓氏命名此算法。 下面直接给出 KMP算法 的操作流程： 1.假设现在文本串 S 匹配到 i 位置，模式串 P 匹配到 j 位置。 2.如果 j = -1，或者当前字符匹配成功（即 S[i] == P[j] ），都令 i++，j++，继续匹配下一个字符。 3.如果 j != -1，且当前字符匹配失败（即 S[i] != P[j] ），则令 i 不变，j = next[j]。此举意味着失配时，模式串 P相对于文本串 S 向右移动了 j - next [j] 位。 4.换言之，将模式串 P 失配位置的 next 数组的值对应的模式串 P 的索引位置移动到失配处。

https://linux.thai.net/~thep/datrie/datrie.html

HSTS 是 HTTP 严格传输安全（HTTP Strict Transport Security） 的缩写。 这是一种网站用来声明他们只能使用安全连接（HTTPS）访问的方法。 如果一个网站声明了 HSTS 策略，浏览器必须拒绝所有的 HTTP 连接并阻止用户接受不安全的 SSL 证书。 目前大多数主流浏览器都支持 HSTS (只有一些移动浏览器无法使用它)。

在协同编辑的产品中广泛应用，各种开源实现在GitHub上都能找到，Google spreadsheet也是基于这项技术

我们经常会拿到一种数据是user—item的表格，然后对应的是每位user对每个item的评分，如下图：

均方误差（MSE） MSE （Mean Squared Error）叫做均方误差

https://github.com/yinqiwen/gscan

什么是OpenTelemetry？ OpenTelemetry合并了OpenTracing和OpenCensus项目，提供了一组API和库来标准化遥测数据的采集和传输。OpenTelemetry提供了一个安全，厂商中立的工具，这样就可以按照需要将数据发往不同的后端。

拼写错误检查工具 https://github.com/hunspell/hunspell

https://grpc.io/blog/a-short-introduction-to-channelz/

https://github.com/envoyproxy/protoc-gen-validate

解决方法： 　　让请求先通过charles，charles再转发给surge。 　　指定http(s)代理端口为charles，charles设置外部代理为surge。最终访问网络的是surge，charles作为前置代理。 　　 首先查看surge /activity，如下界面 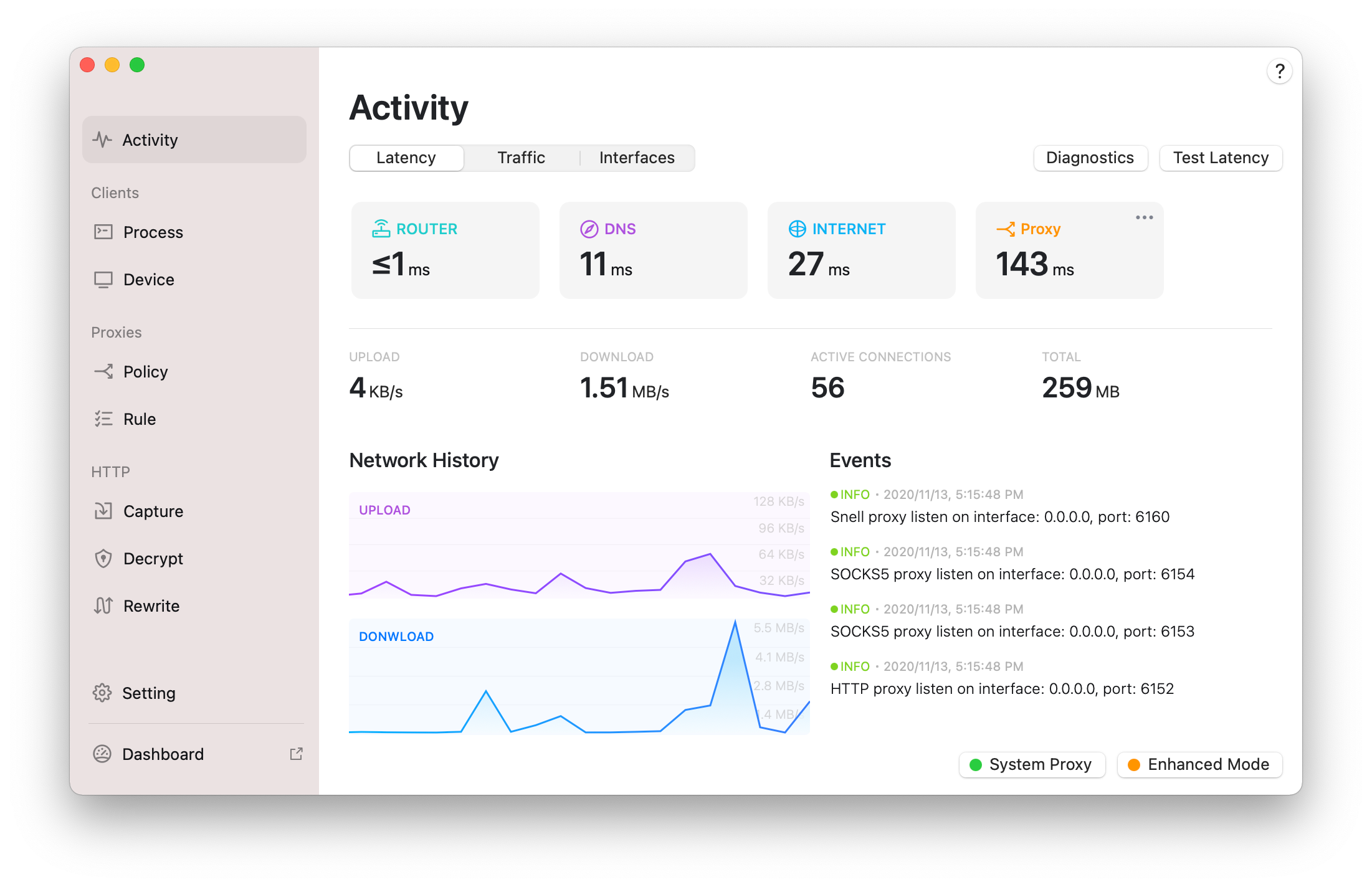可以看到sureg http的代理端口 http 6152，sockets 6153 　1、获取charles监听端口 　2、打开系统Network配置，advanced，proxies，配置HTTP(S)的代理服务器为charles：端口 8888 　 　打开charles的external proxy settings，配置http(s)的外部代理地址为surge：6152 　配置socket 为 6153

http://www.anyconnect.net/

yield* 后面接受一个 iterable object 作为参数，然后去迭代（iterate）这个迭代器（iterable object），同时 yield* 本身这个表达式的值就是迭代器迭代完成时（done: true）的返回值。调用 generator function 会返回一个 generator object，这个对象本身也是一种 iterable object，所以，我们可以使用 yield* generator_function() 这种写法。 yield 是为了解决 node.js 异步回调问题，主要是写法上的同步

node中Promise使用实例 需求：现有三个文件需要依次读取文件内容

class Base{ constructor(arg1,arg2){ this.arg1 = arg1; this.arg2 = arg2; }

configure in doc/example fails with “cannot find install-sh, install.sh, or shtool in “.” “./..” “./../..”” when autoconf is used

https://www.infoq.cn/theme/13 https://github.com/dastergon/awesome-chaos-engineering https://principlesofchaos.org/ https://www.e-learn.cn/topic/3144969

https://www.zhihu.com/question/41109030

https://gocn.vip/topics/11048 https://juejin.im/post/6877505132620333064

he open-source Sourcegraph browser extension adds code intelligence to files and diffs on GitHub, GitHub Enterprise, GitLab, Phabricator, and Bitbucket Server.

《In Search of an Understandable Consensus Algorithm》这个论文中写的比较详细

图片处理在前端工作中可谓占据了很重要的一壁江山。而图片的 base64 编码可能相对一些人而言比较陌生，本文不是从纯技术的角度去讨论图片的 base64 编码。标题略大，不过只是希望通过一些浅显的论述，让你知道什么是图片的 base64 编码，为什么我们要用它，我们如何使用并且方便的使用它，并让你懂得如何去在前端的实际工作中运用它。

1 产生背景

Package 节点表示一组源文件，共同构建 Go 包。

https://algorithm-visualizer.org/dynamic-programming/floyd-warshalls-shortest-path https://github.com/algorithm-visualizer/algorithm-visualizer/wiki https://github.com/xiazemin/algorithm-visualizer https://github.com/xiazemin/fucking-algorithm/tree/master/%E9%AB%98%E9%A2%91%E9%9D%A2%E8%AF%95%E7%B3%BB%E5%88%97 https://github.com/xiazemin/fucking-algorithm

官网创建Flink项目有两种方式：

与Open-Falcon的异同 由于Nightingale与Open-Falcon有很深的血缘关系，想必大家对二者的对比会较为感兴趣。总体来看，理念上有很强的延续性，架构和产品体验上的改进巨大。

https://www.cnblogs.com/sunsky303/p/12957078.html Golang程序调试工具介绍(gdb vs dlv) 通过log库输出日志，我们可以对程序进行异常分析和问题追踪。但有时候，我也希望能有更直接的程序跟踪及定位工具能够帮助我们更方便快捷的追踪、定位问题，最直观的感觉还是使用调试器。Linux平台下，原生的C/C++程序，我们往往使用gdb进行程序调试，切换到Golang，我们同样还是可以使用gdb进行调试。同时我们还可以使用golang实现的调试器dlv进行调试。以下内容是我对gdb以及dlv使用及对比总结 安装 go get github.com/go-delve/delve/cmd/dlv 准备工作 为展示整个调试过程，准备了一个演示项目GoDbg,整个目录结构如下所示

JKHX300590-eyJsaWNlbnNlSWQiOiJKS0hYMzAwNTkwIiwibGljZW5zZWVOYW1lIjoiTmljb2xlIFBvd2VsbCIsImFzc2lnbmVlTmFtZSI6IiIsImFzc2lnbmVlRW1haWwiOiIiLCJsaWNlbnNlUmVzdHJpY3Rpb24iOiJGb3IgZWR1Y2F0aW9uYWwgdXNlIG9ubHkiLCJjaGVja0NvbmN1cnJlbnRVc2UiOmZhbHNlLCJwcm9kdWN0cyI6W3siY29kZSI6IklJIiwicGFpZFVwVG8iOiIyMDE5LTA5LTI0In0seyJjb2RlIjoiQUMiLCJwYWlkVXBUbyI6IjIwMTktMDktMjQifSx7ImNvZGUiOiJEUE4iLCJwYWlkVXBUbyI6IjIwMTktMDktMjQifSx7ImNvZGUiOiJQUyIsInBhaWRVcFRvIjoiMjAxOS0wOS0yNCJ9LHsiY29kZSI6IkdPIiwicGFpZFVwVG8iOiIyMDE5LTA5LTI0In0seyJjb2RlIjoiRE0iLCJwYWlkVXBUbyI6IjIwMTktMDktMjQifSx7ImNvZGUiOiJDTCIsInBhaWRVcFRvIjoiMjAxOS0wOS0yNCJ9LHsiY29kZSI6IlJTMCIsInBhaWRVcFRvIjoiMjAxOS0wOS0yNCJ9LHsiY29kZSI6IlJDIiwicGFpZFVwVG8iOiIyMDE5LTA5LTI0In0seyJjb2RlIjoiUkQiLCJwYWlkVXBUbyI6IjIwMTktMDktMjQifSx7ImNvZGUiOiJQQyIsInBhaWRVcFRvIjoiMjAxOS0wOS0yNCJ9LHsiY29kZSI6IlJNIiwicGFpZFVwVG8iOiIyMDE5LTA5LTI0In0seyJjb2RlIjoiV1MiLCJwYWlkVXBUbyI6IjIwMTktMDktMjQifSx7ImNvZGUiOiJEQiIsInBhaWRVcFRvIjoiMjAxOS0wOS0yNCJ9LHsiY29kZSI6IkRDIiwicGFpZFVwVG8iOiIyMDE5LTA5LTI0In0seyJjb2RlIjoiUlNVIiwicGFpZFVwVG8iOiIyMDE5LTA5LTI0In1dLCJoYXNoIjoiMTAzMTY2ODUvMCIsImdyYWNlUGVyaW9kRGF5cyI6MCwiYXV0b1Byb2xvbmdhdGVkIjpmYWxzZSwiaXNBdXRvUHJvbG9uZ2F0ZWQiOmZhbHNlfQ==-GvkOuUgCVPdyynFuSG+GNmcDZKp643apInM159fRXb69urSBIFyKO46umkRbl89lwr25SrAcl2TfRG1NMP/zPMRmGvd5VHiXDxa/xatzyPpkGf/czv0GeyuP/XhfX8332kXh9Dnowt3Z++IKUlkTjYInkpg09G9OHSwYcIcHAZ51CsqbrWIaemvDH3P9v+k6EUwwhgDZYA/TplavU/2d9J0EZg8kwzo/TK5P7Za09RFx91YBE558Ncl6VMgdhcwgF+oYHGEfs4Bez5xawJwagLymf3mLhq9acihxGnFsfqcyM/EeKDLKWOAveLQIk1NhtU7YR3fFC0EHEGwb04MavA==-MIIEPjCCAiagAwIBAgIBBTANBgkqhkiG9w0BAQsFADAYMRYwFAYDVQQDDA1KZXRQcm9maWxlIENBMB4XDTE1MTEwMjA4MjE0OFoXDTE4MTEwMTA4MjE0OFowETEPMA0GA1UEAwwGcHJvZDN5MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEAxcQkq+zdxlR2mmRYBPzGbUNdMN6OaXiXzxIWtMEkrJMO/5oUfQJbLLuMSMK0QHFmaI37WShyxZcfRCidwXjot4zmNBKnlyHodDij/78TmVqFl8nOeD5+07B8VEaIu7c3E1N+e1doC6wht4I4+IEmtsPAdoaj5WCQVQbrI8KeT8M9VcBIWX7fD0fhexfg3ZRt0xqwMcXGNp3DdJHiO0rCdU+Itv7EmtnSVq9jBG1usMSFvMowR25mju2JcPFp1+I4ZI+FqgR8gyG8oiNDyNEoAbsR3lOpI7grUYSvkB/xVy/VoklPCK2h0f0GJxFjnye8NT1PAywoyl7RmiAVRE/EKwIDAQABo4GZMIGWMAkGA1UdEwQCMAAwHQYDVR0OBBYEFGEpG9oZGcfLMGNBkY7SgHiMGgTcMEgGA1UdIwRBMD+AFKOetkhnQhI2Qb1t4Lm0oFKLl/GzoRykGjAYMRYwFAYDVQQDDA1KZXRQcm9maWxlIENBggkA0myxg7KDeeEwEwYDVR0lBAwwCgYIKwYBBQUHAwEwCwYDVR0PBAQDAgWgMA0GCSqGSIb3DQEBCwUAA4ICAQC9WZuYgQedSuOc5TOUSrRigMw4/+wuC5EtZBfvdl4HT/8vzMW/oUlIP4YCvA0XKyBaCJ2iX+ZCDKoPfiYXiaSiH+HxAPV6J79vvouxKrWg2XV6ShFtPLP+0gPdGq3x9R3+kJbmAm8w+FOdlWqAfJrLvpzMGNeDU14YGXiZ9bVzmIQbwrBA+c/F4tlK/DV07dsNExihqFoibnqDiVNTGombaU2dDup2gwKdL81ua8EIcGNExHe82kjF4zwfadHk3bQVvbfdAwxcDy4xBjs3L4raPLU3yenSzr/OEur1+jfOxnQSmEcMXKXgrAQ9U55gwjcOFKrgOxEdek/Sk1VfOjvS+nuM4eyEruFMfaZHzoQiuw4IqgGc45ohFH0UUyjYcuFxxDSU9lMCv8qdHKm+wnPRb0l9l5vXsCBDuhAGYD6ss+Ga+aDY6f/qXZuUCEUOH3QUNbbCUlviSz6+GiRnt1kA9N2Qachl+2yBfaqUqr8h7Z2gsx5LcIf5kYNsqJ0GavXTVyWh7PYiKX4bs354ZQLUwwa/cG++2+wNWP+HtBhVxMRNTdVhSm38AknZlD+PTAsWGu9GyLmhti2EnVwGybSD2Dxmhxk3IPCkhKAK+pl0eWYGZWG3tJ9mZ7SowcXLWDFAk0lRJnKGFMTggrWjV8GYpw5bq23VmIqqDLgkNzuoog== https://xclient.info/s/clion.html#versions

利益相关：基本上只用Theano。跟Theano的最早的lead developers之一比较熟。速度上：Theano的compile是慢的。这取决于computation graph的结构。Running速度是可以的（相对而言只能说OK，soumith/convnet-benchmarks · GitHub）。Parallel以及data loading和是蛋疼的。其中Cpython中的global interpreter lock居功至伟。关于好用不好用：先说缺点，debug是困难的。往往需要推测才知道具体是哪里出了问题。如果说是做标准的结构，有keras，lasagne，blocks，pylearn2等等库的支持，实现起来非常容易。如果说是方便灌水了。那torch，caffe或者whatever toolbox https://www.zhihu.com/question/35485591 https://morvanzhou.github.io/tutorials/machine-learning/theano/ http://www.deeplearning.net/software/theano/ https://pypi.org/project/Theano/

https://www.cnblogs.com/FireworksEasyCool/p/12750339.html gRPC中TLS认证和自定义方法认证，最后还简单介绍了gRPC拦截器的使用。gRPC自身只能设置一个拦截器，所有逻辑都写一起会比较乱。本篇简单介绍go-grpc-middleware的使用，包括grpc_zap、grpc_auth和grpc_recovery。

我们所面对的数据是海量的，并且有着很高的维度。在对数据的各种操作中，查询操作是最常见的一种，这里的查询是指输入一个数据，查找与其相似的数据，那么怎样快速地从海量高维数据中，找到与某个数据最相似的数据，成为了一个难点和问题。

频次限制（rate limiting）是Web系统比较常见的功能，防止用户频繁访问接口，导致系统负载增加而影响服务的质量。

https://segmentfault.com/a/1190000022288698 一、字典 字典是存储键值对的数据结构，把一个键和一个值映射起来，一一映射，键不能重复。在某些教程中，这种结构可能称为符号表，关联数组或映射。我们暂且称它为字典，较好理解。 如：

https://segmentfault.com/a/1190000022288951 一、线性查找 我们要通过一个键key来查找相应的值value。有一种最简单的方式，就是将键值对存放在链表里，然后遍历链表来查找是否存在key，存在则更新键对应的值，不存在则将键值对链接到链表上。

https://segmentfault.com/a/1190000022367093 2-3-4树和普通红黑树 某些教程不区分普通红黑树和左倾红黑树的区别，直接将左倾红黑树拿来教学，并且称其为红黑树，因为左倾红黑树与普通的红黑树相比，实现起来较为简单，容易教学。在这里，我们区分开左倾红黑树和普通红黑树。

edis中一个db就是一个大dict，也就是实现的可伸缩hash表。其操作支持遍历scan类操作，按stl容器中场景的逻辑，如果一个迭代器在迭代过程中被修改(插入或删除)元素，迭代器可能失效。

Map：在数组中是通过数组下标来对 其内容进行索引的，而Map是通过对象来对 对象进行索引的，用来 索引的对象叫键key，其对应的对象叫值value；

不管我们是不是有身份的人，我们一定是有身份证的人，身份证上面的号码就是我们的ID，理论上这个ID是全国唯一的，而且通过这个号码，我们还可以得到一些个人信息，比如前两位可以确定我们第一次申请身份证的时候所在的省份、接下来的四位可以确定我们所在的区县，然后还可以知道我们出生的年月以及性别。

https://gocn.vip/topics/10135 重试解决什么问题 短时故障的产生原因 处理短时故障的挑战 重试分为几步 gRPC 是如何进行重试的

1. 重试解决什么问题 如今的互联网服务早已不是单体应用，而是由若干个模块组成的微服务，每个模块可以进行单独的扩容、缩容，独立上线部署等等；模块与模块之间通过网络进行联通。我们的应用必须对网络错误进行妥善的处理。从发生时长上而言，网络错误可以分为两类：

https://gocn.vip/topics/10015 单台服务器处理能力越来越强，迫使编程模式由从前的串行模式升级到并发模型。

https://mp.weixin.qq.com/s/cdRjQdgaA6Z9x8UZgGTN2Q 多年来，API管理（API Management，APIM）–以及API网关的采用–是用于在数据中心内外实现现代API用例的主要技术。API网关技术在过去十年中有了很大的发展，在业界所谓的“全生命周期API管理”中获得了更大、更全面的用例。不仅是运行时在请求的数据平面上连接、保护和管理我们的API流量，而且还具有一系列功能，可以在更广泛的范围内创建、测试、文档化、收费、监控和全面暴露API–并从头到尾针对更广泛的用户角色。也就是说，这里存在一个完整的生命周期，即创建API并将其作为产品提供给用户和客户，而不仅仅是网络运行时的管理，这使我们能够暴露和使用API（不管是否使用RESTful）。

1.是什么 1.1 Goroutine的定义 A Tour of Go给出的官方定义是：

DDD：四色原型、DDD、DCI之间的关系 PPT对应某个聚合。 Des对应某个聚合或其它聚合内的实体或值对象。 MI对应某个聚合。 Role对应PPT（Data）在某个上下文（Context）执行某些交互（Interactive）的代理或装饰器。 四色原型中的一些静态方法需要移动到仓储或服务中。 https://www.jdon.com/ddd.html

https://www.ibm.com/developerworks/cn/java/j-javaactors/

Data, Context and Interaction : A New Architectural Approach by James O. Coplien and Trygve Reenskau

golang中的切片slice底层通过数组实现，slice类似一个结构体，其中一个字段保存的是底层数组的地址，还有长度(len) 和 容量(cap）两个字段。

https://conroy.org/introducing-sqlc https://github.com/kyleconroy/sqlc

一、前言 前几天的工作中，需要通过curl做一次接口测试。让我意外的是，通过$_POST竟然无法获取到Content-Type是application/json的http请求的body参数。 查了下php官网（http://php.net/manual/zh/reserved.variables.post.php）对$_POST的描述，的确是这样。后来通过file_get_contents(“php://input”)获取到了原始的http请求body，然后对参数进行json_decode解决了接口测试的问题。事后，脑子里面冒出了挺多问题：

如何存储密码才是安全的？ 密码存储有几种方式：

公开密钥基础建设（英语：Public Key Infrastructure，缩写：PKI），又称公开密钥基础架构、公钥基础建设、公钥基础设施、公开密码匙基础建设或公钥基础架构，是一组由硬件、软件、参与者、管理政策与流程组成的基础架构，其目的在于创造、管理、分配、使用、存储以及撤销数字证书。

不一定非要自己存储用户的密码 最简单的存储密码的方式就是自己并不存储，而是委托给信任的第三方存储。这就是OpenID技术，它的理念是用第三方来完成用户验证的操作。目前国外的网站如谷歌、雅虎等，国内的如腾讯等都已经提供OpenID的服务。如果我们开发一个网站并选择谷歌的OpenID服务，那么用户就可以用Gmail的账号和密码登录，接下来用户认证的事情将由谷歌完成。

近日，Kubernetes 1.13 正式发布，这是 2018 年发布的第四次也是最后一次大版本，该版本继续关注 Kubernetes 稳定性和可扩展性，对存储和集群生命周期的主要功能实现高可用。Kubeadm 简化了集群管理、容器存储接口（CSI）并将 CoreDNS 作为默认 DNS。

kmp 用来查找目标串在模式串中的位置 ac 自动机与之对应，用来查找目标串中是否包含，模式串 两者有很多相似性，比如kmp的next数组和ac自动机的fail指针类似，只不过，前者用来匹配相同前缀，后者用来匹配相同后缀（从root出发，包含途径匹配）

实现 strStr() 函数。 给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

https://oi-wiki.org/string/ac-automaton/ AC 自动机是 以 TRIE 的结构为基础 ，结合 KMP 的思想 建立的。

原型

https://github.com/istio/istio https://www.servicemesher.com/blog/back-to-microservices-with-istio-p1/ 在微服务架构中，服务可能会用不同的语言实现并部署在多个节点或集群上，具有不同的响应时间或故障率。如果服务成功（并且及时地）响应了请求，那么它的性能就算是令人满意的。但现实情况并非如此，下游客户端应该在上游服务过于缓慢时受到保护。反之，上游服务也必须被保护，以免被积压的请求拖垮。在多客户端下情况会更加复杂，并可能导致整个基础设施出现一系列的连锁故障。这一问题的解决方案是采用经过时间检验的熔断器模式。

https://github.com/qichengzx/coordtransform https://github.com/wandergis/coordtransform

将事件点数据聚合到形状规则格网的原因很多，如正规化地理制图或减少因使用随意创建的不规则面而出现的问题（如通过政治流程创建的县边界或区块组）。规则形状格网仅可由等边三角形、正方形或六边形组成，因为只有这三种多边形形状可以进行镶嵌（使用相同的形状重复地拼接，以无缝或无重叠覆盖一块区域）以创建均匀的格网。 尽管正方形（渔网）格网是 GIS 分析和专题制图中主要使用的形状类型，根据您问题的性质，六边形在某些情况下更适合进行分析。

https://github.com/golang/geo https://github.com/uber/h3-go

动态空间划分（R-tree） 静态空间划分（GeoHash、google S2、uber H3） 四叉树 经度、纬度的二分来分块，逻辑最简单。 Z-行空间遍历 编码方式 所在层级经纬度二分下标（0、1），先经后纬，逐层排列。

https://github.com/xiazemin/h3-go https://uber.github.io/h3/#/documentation/overview/introduction https://uber.github.io/h3/#/documentation/core-library/coordinate-systems https://halfrost.com/go_spatial_search/ https://github.com/vraid/earthgen-old https://gist.github.com/jp1017/71bd0976287ce163c11a7cb963b04dd8

对于长整型数据的映射。怎样解决Hash冲突和Hash表大小的设计是一个非常头疼的问题。 radix树就是针对这样的稀疏的长整型数据查找，能高速且节省空间地完毕映射。借助于Radix树，我们能够实现对于长整型数据类型的路由。 利用radix树能够依据一个长整型（比方一个长ID）高速查找到其相应的对象指针。这比用hash映射来的简单，也更节省空间，使用hash映射hash函数难以设计，不恰当的hash函数可能增大冲突，或浪费空间。

自己试验了下rsa https://github.com/xiazemin/rsa golang 只提供了公钥加密私钥解密的算法 晚上找了下私钥签名（加密），公钥验证（解密）的算法

数据签名和数据加密的过程都是使用公开的密钥系统，但实现的过程正好相反，

MD5，全名Message Digest Algorithm 5 ，中文名为消息摘要算法第五版，为计算机安全领域广泛使用的一种散列函数，用以提供消息的完整性保护。 通过特定的hash散列方法将文本信息转换成简短的信息摘要，压缩+加密+hash算法的结合体，是绝对不可逆的。 二、MD5计算步骤   

图的连通性判断方法主要有：并查集、DFS、BFS、WARSHALL 一、并查集

GIMPLE中间表示，是GCC中机器无关的中间表示，机器无关的优化基本都在这个层次上做。 http://gcc.gnu.org/onlinedocs/gccint/GIMPLE.html 在编译过程中，GCC使用了三种主要的中间语言来表示程序：GENERIC，GIMPLE和RTL。GENERIC是一种由每个前端生成的语言无关的表示。它用来作为解析器和优化器之间的接口。GENERIC是一种通用表示，能够表示GCC支持的所有语言程序。

 Treap=Tree+Heap。Treap是一棵二叉排序树，它的左子树和右子树分别是一个Treap，和一般的二叉排序树不同的是, Treap记录一个额外的数据， 就是优先级。Treap在以关键码构成二叉排序树的同时，还满足堆的性质(在这里我们假设节点的优先级大于该节点的孩子的优先级)。但是这里要注意的是Treap和二叉堆有一点不同，就是 二叉堆必须是完全二叉树，而Treap不一定是完全二叉树。 在二叉查找树中，当插入的数据为随机的时候，其有较好的性能使得孩子节点大体上左右均匀分布。但是，当插入的数据为有序的时候，其会退化为一个链表的状态，从而达不到效果。一般，我们有AVL或者红黑树以及Splay等平衡二叉树结构。但是，其在实现上难度较高。为此，引入了Treap，treap采用了二叉堆的性质来保持二叉树的平衡性。因为对于一个堆而言，其需要满足如下的性质：一个节点的两个孩子节点的值都小于节点的本身的值。但是，对于一棵二叉查找树而言，其需要满足一棵树的左孩子节点的值小于根节点的值并且右孩子节点的值大于根节点的值。这显然出现了冲突。为此，我们需要增加一个变量，用于满足这样的性质。我们将用于满足二叉搜索树的性质的值称之为key，用于满足堆的性质的值称之为priority(优先级)。

The Sieve of Eratosthees 爱拉托逊斯筛选法思想：对于不超过n的每个非负整数P，删除2P, 3P…，当处理 完所有数之后，还没有被删除的就是素数。 若用vis==1表示已被删除，则代码如下： memset(vis, 0, sizeof(vis)); for(int i = 2; i <= 100; i++) for(int j = i*2; j <= 100; j += i) vis[j] = 1; 改进的代码： int m = sqrt(double(n+0.5));

compareAndSet方法的实现很简单，只有一行代码。这里涉及到两个重要的对象，一个是unsafe，一个是valueOffset。

　谈到并发，不得不谈ReentrantLock；而谈到ReentrantLock，不得不谈AbstractQueuedSynchronizer（AQS）！

HashMap:HashMap数据是无序的，根据键的hashCode进行数据的存取，对数据的访问速度非常快，在map中插入删除

一批测试服务器，之间希望通过自定义的域名进行访问，这样比较方便，但每个人每台机器都维护一个hosts的话会非常麻烦，于是想搭建一个内部的DNS服务器，对自定义的域名进行解析，同时缓存公网的域名。

LVS（Linux Virtual Server）即Linux虚拟服务器，是一个虚拟的服务器集群系统 实现负载均衡一般可以使用顺序、比重、流量、服务类别等进行分配，负载均衡的部署方式也分为路由和服务直接返回模式，实现负载均衡的主要几个方式： http重定向 下载网站用的较多，其实也算一种负载均衡，工作在应用层的业务代码中 DNS负载均衡 DNS负载提供域名到IP解析的过程，我们实例查看百度的域名解析其实是一对多的，这时候DNS服务器也就充当了负载均衡，很多域名运营商提供的智能dns以及多线解析都是利用了DNS负载均衡的技术，开源的BIND就可提供电信联通多线解析等强大的技术。 反向代理负载均衡

SnowFlake算法生成id的结果是一个64bit大小的整数 1位，不用。二进制中最高位为1的都是负数，但是我们生成的id一般都使用整数，所以这个最高位固定是0 41位，用来记录时间戳（毫秒）。

Feature Consul zookeeper etcd euerka 服务健康检查 服务状态，内存，硬盘等 (弱)长连接，keepalive 连接心跳 可配支持 多数据中心 支持 — — — kv存储服务 支持 支持 支持 — 一致性 raft paxos raft — cap cp cp cp ap 使用接口(多语言能力) 支持http和dns 客户端 http/grpc http（sidecar） watch支持 全量/支持long polling 支持 支持long polling 支持 long polling/大部分增量 自身监控 metrics — metrics metrics 安全 acl /https acl https支持（弱） — spring cloud集成 已支持 已支持 已支持 已支持 Eureka是一个服务发现工具。该体系结构主要是客户端/服务器，每个数据中心有一组Eureka服务器，通常每个可用区域一个。通常Eureka的客户使用嵌入式SDK来注册和发现服务。对于非本地集成的客户，使用功能区边框等透过Eureka透明地发现服务。

maxmemory 用于指定 Redis 能使用的最大内存。既可以在 redis.conf 文件中设置, 也可以在运行过程中通过 CONFIG SET 命令动态修改。 将 maxmemory 设置为 0, 则表示不进行内存限制。当然, 对32位系统来说有一个隐性的限制条件: 最多 3GB 内存。

因为大量的数据库（如MySQL、oracle、PostgreSQL等）都在使用B树。B树索引本质上是对索引字段进行排序，然后通过类似二分查找的方法进行快速查找，即它要求索引的字段是可排序的，一般而言，可排序的是一维字段，比如时间、年龄、薪水等等。但是对于空间上的一个点（二维，包括经度和纬度），如何排序呢？又如何索引呢？ 如果能通过某种方法将二维的点数据转换成一维的数据，那样不就可以继续使用B树索引了嘛。那这种方法真的存在嘛，答案是肯定的。目前很火的GeoHash算法就是运用了上述思想 http://openlocation.org/geohash/geohash-js/ 提供了在地图上显示geohash编码的功能。 1）GeoHash将二维的经纬度转换成字符串，比如9个区域的GeoHash字符串，分别是WX4ER，WX4G2、WX4G3等等，每一个字符串代表了某一矩形区域。也就是说，这个矩形区域内所有的点（经纬度坐标）都共享相同的GeoHash字符串，这样既可以保护隐私（只表示大概区域位置而不是具体的点），又比较容易做缓存，比如左上角这个区域内的用户不断发送位置信息请求餐馆数据，由于这些用户的GeoHash字符串都是WX4ER，所以可以把WX4ER当作key，把该区域的餐馆信息当作value来进行缓存，而如果不使用GeoHash的话，由于区域内的用户传来的经纬度是各不相同的，很难做缓存。 2）字符串越长，表示的范围越精确。如图所示，5位的编码能表示10平方千米范围的矩形区域，而6位编码能表示更精细的区域（约0.34平方千米） 3）字符串相似的表示距离相近（特殊情况后文阐述），这样可以利用字符串的前缀匹配来查询附近的POI信息。一个在城区，一个在郊区，城区的GeoHash字符串之间比较相似，郊区的字符串之间也比较相似，而城区和郊区的GeoHash字符串相似程度要低些。 在大部分情况下，字符串前缀匹配越多的距离越近，回到我们的案例，根据所在位置查询来查询附近餐馆时，只需要将所在位置经纬度转换成GeoHash字符串，并与各个餐馆的GeoHash字符串进行前缀匹配，匹配越多的距离越近。

跳表是一种随机化的数据结构，目前开源软件 Redis 和 LevelDB 都有用到它，

在并发程序中，串行操作是会降低可伸缩性，并且上下文切换也会减低性能。在锁上发生竞争时将通水导致这两种问题，使用独占锁时保护受限资源的时候，基本上是采用串行方式—-每次只能有一个线程能访问它。所以对于可伸缩性来说最大的威胁就是独占锁。

什么是异地多活 异地多活一般是指在不同城市建立独立的数据中心，“活”是相对于冷备份而言的，冷备份是备份全量数据，平时不支撑业务需求，只有在主机房出现故障的时候才会切换到备用机房，而多活，是指这些机房在日常的业务中也需要走流量，做业务支撑。冷备份的主要问题是成本高，不跑业务，当主机房出问题的时候，也不一定能成功把业务接管过来。

基于整数线性规划(ILP)方法 将摘要看做一个带约束的优化问题 基于ILP进行求解，可采用现成的ILP求解工具 同时进行句子抽取与冗余去除  python下ILP求解工具学习： 使用流程 　　我们解决线性规划问题一般是通过以下三个步骤。 1.列出约束条件及目标函数 2.画出约束条件所表示的可行域 使用pulp工具包，我们只需要做第一步即可，使用pulp提供的API提供目标函数及约束条件就可以直接求解，非常方便。  　

Network Time Protocol （网络时间协议）是 GNU/Linux 系统通过互联网时间服务器同步系统软件时钟的最常见方法。设计时考虑到了各种网络延迟，通过公共网络同步时，误差可以降低到10毫秒以内；通过本地网络同步时，误差可以降低到 1 毫秒。 配置 主要的后台进程是 ntpd, 可以通过 /etc/ntp.conf 配置。详细信息可以参考手册 ntp.conf(5) 和相关的 man {ntpd|ntp_auth|ntp_mon|ntp_acc|ntp_clock|ntp_misc}.

计算机科学的方法并没有使用离散数学的模型来模拟一个地理信息系统(GIS)–而是建模出了一个我们真是存在的物理空间框架。实际上，大家已经接受了传统使用的球形的坐标或者凸的笛卡尔坐标系。因为这这些模型定义的是连续的点，而不是离散的一片一片，所以我们称这些模型为模拟地理参考模型（Analog Earth Reference Models）。

R树是B树 向多维空间发展的另一种形式，它将对象空间按范围划分，每个结点都对应一个区域和一个磁盘页，非叶结点的磁盘页中存储其所有子结点的区域范围，非叶结点的 所有子结点的区域都落在它的区域范围之内；叶结点的磁盘页中存储其区域范围之内的所有空间对象的外接矩形。R树是一种动态索引结构。 （1）R-Tree是n 叉树，n称为R-Tree的扇（fan）。 （2）每个结点对应一个矩形。 （3）叶子结点上包含了小于等于n 的对象，其对应的矩为所有对象的外包矩形。 （4）非叶结点的矩形为所有子结点矩形的外包矩形。 R-Tree的定义很宽泛，同一套数据构造R-Tree，不同方可以得到差别很大的结构。什么样的结构比较优呢？有两标准： （1）位置上相邻的结点尽量在树中聚集为一个父结点。 （2）同一层中各兄弟结点相交部分比例尽量小。 R-树是一种用于处理多维数据的数据结构，用来访问二维或者更高维区域对象组成的空间数据.R树是一棵平衡树。树上有两类结点：叶子结点和非叶子结点。每一个结点由若干个索引项构成。对于叶子结点，索引项形如(Index，Obj_ID)。其中，Index表示包围空间数据对象的最小外接矩形MBR，Obj_ID标识一个空间数据对象。对于一个非叶子结点，它的索引项形如(Index，Child_Pointer)。 Child_Pointer 指向该结点的子结点。Index仍指一个矩形区域，该矩形区域包围了子结点上所有索引项MBR的最小矩形区域。 符号说明：M：结点中单元的最大数目，m(1<= m <= M/2)为非根结点中单元个数的下限。 一个R树满足如下性质: (1) 每一个叶子结点中包含的单元的个数介于m和M之间，除非他同样是根结点 (2) 每一个叶子结点中的单元(I, tuple-identifier),I为包含所有子结点的最小包含矩形(MBR)，tuple-identifier是指向存储记录的指针。 (3) 每一个非叶子结点的子结点数介于m和M之间，除非他是根结点 (4) 每一个非叶子结点单元(I, child -pointer)I是包含子结点的最小矩形MBR，child-pointer是指向子结点的指针。通过该指针逐层递归，可以访问到叶子结点。 (5) 根结点至少有两个子结点，除非他同时是叶子结点 (6) 所有的叶子结点都处在树的同一层上。 算法描述编辑 算法描述如下： 对象数为n，扇区大小定为fan。 （1）估计叶结点数k=n/fan。 （2）将所有几何对象按照其矩形外框中心点的x值排序。 （3）将排序后的对象分组，每组大小为 fan，最后一组可能不满员。 （4）上述每一分组内按照几何对象矩形外框中心点的y值排序。 （5）排序后每一分组内再分组，每组大小为fan。 （6）每一小组成为叶结点，叶子结点数为nn。 （7）k=nn，返回1。 其他索引结构编辑 R+树 在Guttman的工作的基础上，许多R树的变种被开发出来， Sellis等提出了R+树 [4] ，R+树与R树类似，主要区别在于R+树中兄弟结点对应的空间区域无重叠，这样划分空间消除了R树因允许结点间的重叠而产生的“死区域”（一个结点内不含本结点数据的空白区域），减少了无效查询数，从而大大提高空间索引的效率，但对于插入、删除空间对象的操作，则由于操作要保证空间区域无重叠而效率降低。同时R+树对跨区域的空间物体的数据的存储是有冗余的，而且随着数据库中数据的增多，冗余信息会不断增长。Greene也提出了他的R树的变种。 R树 在1990年，Beckman和Kriegel提出了最佳动态R树的变种——R树 [4] 。R树和R树一样允许矩形的重叠，但在构造算法R树不仅考虑了索引空间的“面积”，而且还考虑了索引空间的重叠。该方法对结点的插入、分裂算法进行了改进，并采用“强制重新插入”的方法使树的结构得到优化。但R树算法仍然不能有效地降低空间的重叠程度，尤其是在数据量较大、空间维数增加时表现的更为明显。R树无法处理维数高于20的情况。 QR树 QR树 [5] 利用四叉树将空间划分成一些子空间，在各子空间内使用许多R树索引，从而改良索引空间的重叠。QR树结合了四叉树与R树的优势，是二者的综合应用。实验证明：与R树相比，QR树以略大（有时甚至略小）的空间开销代价，换取了更高的性能，且索引目标数越多，QR树的整体性能越好。 SS树 SS树对R树进行了改进，通过以下措施提高了最邻近查询的性能：用最小边界圆代替最小边界矩形表示区域的形状，增强了最邻近查询的性能，减少将近一半存储空间；SS树改进了R树的强制重插机制。当维数增加到5是，R树及其变种中的边界矩形的重叠将达到90%，因此在高维情况（≧5）下，其性能将变的很差，甚至不如顺序扫描。 X树 X树 [6] 是线性数组和层状的R树的杂合体，通过引入超级结点，大大地减少了最小边界矩形之间的重叠，提高了查询效率。X树用边界圆进行索引，边界矩形的直径（对角线）比边界圆大，SS树将点分到小直径区域。由于区域的直径对最邻近查询性能的影响较大，因此SS树的最邻近查询性能优于R树；边界矩形的平均容积比边界圆小，R树将点分到小容积区域；由于大的容积会产生较多的覆盖，因此边界矩形在容积方面要优于边界圆。SR树既采用了最小边界圆（MBS），也采用了最小边界矩形（MBR），相对于SS树，减小了区域的面积，提高了区域之间的分离性，相对于R树，提高了邻近查询的性能。 1984年，加州大学伯克利分校的Guttman发表了一篇题为“R-trees: a dynamic index structure for spatial searching”的论文，向世人介绍了R树这种处理高维空间存储问题的数据结构。 R树在数据库等领域做出的功绩是非常显著的。它很好的解决了在高维空间搜索等问题。举个R树在现实领域中能够解决的例子：查找20英里以内所有的餐厅。如果没有R树你会怎么解决？一般情况下我们会把餐厅的坐标(x,y)分为两个字段存放在数据库中，一个字段记录经度，另一个字段记录纬度。这样的话我们就需要遍历所有的餐厅获取其位置信息，然后计算是否满足要求。如果一个地区有100家餐厅的话，我们就要进行100次位置计算操作了，如果应用到谷歌地图这种超大数据库中，这种方法便必定不可行了。 R树就很好的解决了这种高维空间搜索问题。它把B树的思想很好的扩展到了多维空间，采用了B树分割空间的思想，并在添加、删除操作时采用合并、分解结点的方法，保证树的平衡性。因此，R树就是一棵用来存储高维数据的平衡树。 R树是B树在高维空间的扩展，是一棵平衡树。每个R树的叶子结点包含了多个指向不同数据的指针，这些数据可以是存放在硬盘中的，也可以是存在内存中。根据R树的这种数据结构，当我们需要进行一个高维空间查询时，我们只需要遍历少数几个叶子结点所包含的指针，查看这些指针指向的数据是否满足要求即可。这种方式使我们不必遍历所有数据即可获得答案，效率显著提高。 R树运用了空间分割的理念，这种理念是如何实现的呢？R树采用了一种称为MBR(Minimal Bounding Rectangle)的方法，在此我把它译作“最小边界矩形”。从叶子结点开始用矩形（rectangle）将空间框起来，结点越往上，框住的空间就越大，以此对空间进行分割。 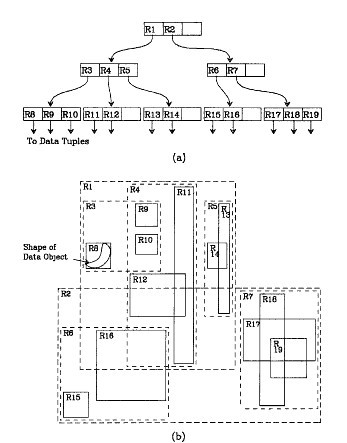先来看图（b），首先我们假设所有数据都是二维空间下的点，图中仅仅标志了R8区域中的数据，也就是那个shape of data object。别把那一块不规则图形看成一个数据，我们把它看作是多个数据围成的一个区域。为了实现R树结构，我们用一个最小边界矩形恰好框住这个不规则区域，这样，我们就构造出了一个区域：R8。R8的特点很明显，就是正正好好框住所有在此区域中的数据。其他实线包围住的区域，如R9，R10，R12等都是同样的道理。这样一来，我们一共得到了12个最最基本的最小矩形。这些矩形都将被存储在子结点中。下一步操作就是进行高一层次的处理。我们发现R8，R9，R10三个矩形距离最为靠近，因此就可以用一个更大的矩形R3恰好框住这3个矩形。同样道理，R15，R16被R6恰好框住，R11，R12被R4恰好框住，等等。所有最基本的最小边界矩形被框入更大的矩形中之后，再次迭代，用更大的框去框住这些矩形。我想大家都应该理解这个数据结构的特征了。用地图的例子来解释，就是所有的数据都是餐厅所对应的地点，先把相邻的餐厅划分到同一块区域，划分好所有餐厅之后，再把邻近的区域划分到更大的区域，划分完毕后再次进行更高层次的划分，直到划分到只剩下两个最大的区域为止。要查找的时候就方便了。

https://www.w3cschool.cn/samza/ Samza介绍 Samza是近日由LinkedIn开源的一项技术，它是一个分布式流处理框架，它是基于Kafka消息队列来实现类实时的流式数据处理的，非常像Twitter的流处理系统Storm。不同的是Samza基于Hadoop，而且使用了LinkedIn自家的Kafka分布式消息系统，并使用资源管理器Apache Hadoop YARN实现容错处理、处理器隔离、安全性和资源管理。

分布式锁一般有三种实现方式：1. 数据库乐观锁；2. 基于Redis的分布式锁；3. 基于ZooKeeper的分布式锁。 我们至少要确保锁的实现同时满足以下四个条件：

1.CMake编译原理

实现原理 数据库连接池在初始化时将创建一定数量的数据库连接放到连接池中，这些数据库连接的数量是由最小数据库连接数制约。无论这些数据库连接是否被使用，连接池都将一直保证至少拥有这么多的连接数量。连接池的最大数据库连接数量限定了这个连接池能占有的最大连接数，当应用程序向连接池请求的连接数超过最大连接数量时，这些请求将被加入到等待队列中。 连接池基本的思想是在系统初始化的时候，将数据库连接作为对象存储在内存中，当用户需要访问数据库时，并非建立一个新的连接，而是从连接池中取出一个已建立的空闲连接对象。使用完毕后，用户也并非将连接关闭，而是将连接放回连接池中，以供下一个请求访问使用。而连接的建立、断开都由连接池自身来管理。同时，还可以通过设置连接池的参数来控制连接池中的初始连接数、连接的上下限数以及每个连接的最大使用次数、最大空闲时间等等。也可以通过其自身的管理机制来监视数据库连接的数量、使用情况等。

著名的CAP理论指出，一个分布式系统不可能同时满足C(一致性)、A(可用性)和P(分区容错性)。由于分区容错性在是分布式系统中必须要保证的，因此我们只能在A和C之间进行权衡。在此Zookeeper保证的是CP, 而Eureka则是AP。

什么是 DNS

iadoz 在 Github 发起维护的一个 PHP 资源列表，内容包括：库、框架、模板、安全、代码分析、日志、第三方库、配置工具、Web 工具、书籍、电子书、经典博文等等。

哈希（hash）是一种非常快的查找方法，一般情况下查找的时间复杂度为O（1）。常用于连接（join）操作，如SQL Server和Oracle中的哈希连接（hash join）。但是SQL Server和Oracle等常见的数据库并不支持哈希索引（hash index）。MySQL的Heap存储引擎默认的索引类型为哈希，而InnoDB存储引擎提出了另一种实现方法，自适应哈希索引（adaptive hash index）。

SDS（Simple Dynamic Strings）是一个C语言字符串库，设计中增加了从堆上分配内存的字符串，来扩充有限的libc字符处理的功能，使得： 这和在你的项目中拷贝sds.c和sds.h文件一样简单。代码很小，每个C99编译器应该都不带任何问题地搞定。 使用更简便 二进制安全 计算更有效率 而且仍旧…兼容一般的C字符串功能 https://github.com/antirez/sds

有序数组可以快速索引，但是增删困难 链表可以快速增删，但是索引困难 结合两者的优点，以时间换空间，用数组索引部分数据，链表存数据，索引还可以多层，或者直接用链表多层索引，就是跳表。 经常使用的平衡数据结构有：B树，红黑树，AVL树，Splay Tree, Treep等。目前开源软件 Redis 和 LevelDB 都有用到它， 它的效率和红黑树以及 AVL 树不相上下，但跳表的原理相当简单。 跳跃表的性质；

https://github.com/aappleby/smhasher 看Jedis的主键分区哈希时，看到了名字很萌很陌陌的MurmurHash，谷歌一看才发现Redis，Memcached，Cassandra，HBase，Lucene都用它。 其实是 multiply and rotate的意思，因为算法的核心就是不断的”x *= m; x = rotate_left(x,r);” MurmurHash算法：高运算性能，低碰撞率，由Austin Appleby创建于2008年，现已应用到Hadoop、libstdc++、nginx、libmemcached等开源系统。2011年Appleby被Google雇佣，随后Google推出其变种的CityHash算法。 官方网站：https://sites.google.com/site/murmurhash/ MurmurHash算法，自称超级快的hash算法，是FNV的4-5倍。

https://github.com/tkem/cachetools https://pypi.org/project/cachetools/ opcache是个提升php性能的利器，但是在线上服务器真实遇到过偶尔几台服务器代码上线后，一直没有生效，查看opcache的配置也没有问题。后来没有办法，就在上线步骤中增加了重启php-fpm的操作。今天发现了一个小工具cachetool。可以方便的使用命令行清除opcache的缓存。 当然除了重启php-fpm的进程可以清理opcache缓存外，opcache本身是支持清除缓存的。手动清理缓存涉及到的opcache函数主要为：opcache_reset()和opcache_invalidate() 。 但是opcache_reset()是php中的函数，需要在php脚本中执行，另外当PHP以PHP-FPM的方式运行的时候，opcache的缓存是无法通过php命令进行清除的，只能通过http或cgi到php-fpm进程的方式来清除缓存。 而opcache_invalidate 废除指定脚本缓存是使指定脚本的字节码缓存失效。可用于明确更新的代码文件列表时使用，但不方便清除整个脚本的缓存。cachetool使用起来也非常方便。如下：

dapper是通过trace tree和span构建跟踪系统的。

influxdb是目前比较流行的时间序列数据库。

OpenStack既是一个社区，也是一个项目和一个开源软件，提供开放源码软件，建立公共和私有云，它提供了一个部署云的操作平台或工具集，其宗旨在于：帮助组织运行为虚拟计算或存储服务的云，为公有云、私有云，也为大云、小云提供可扩展的、灵活的云计算。 OpenStackd开源项目由社区维护，包括OpenStack计算（代号为Nova），OpenStack对象存储（代号为Swift），并OpenStack镜像服务（代号Glance）的集合。 OpenStack提供了一个操作平台，或工具包，用于编排云。 整个OpenStack是由控制节点，计算节点，网络节点，存储节点四大部分组成。（这四个节点也可以安装在一台机器上，单机部署） 其中： 控制节点负责对其余节点的控制，包含虚拟机建立，迁移，网络分配，存储分配等等 计算节点负责虚拟机运行 网络节点负责对外网络与内网络之间的通信 存储节点负责对虚拟机的额外存储管理等等

即使 Java 6 和 Java 7 中引入并发性更新，Java 语言仍然无法让并行编程变得特别容易。Java 线程、synchronized 代码块、wait/notify 和 java.util.concurrent 包都拥有自己的位置，但面对多核系统的容量压力，Java 开发人员正在依靠其他语言中开创的技术。actor 模型就是这样一项技术，它已在 Erlang、Groovy 和 Scala 中实现。 μJavaActors 库 是一个紧凑的库，用于在 Java 平台上实现基于 actor 的系统（μ 表示希腊字母 Mμ，意指 “微型”）。 通过实现一种消息传递 模式，使并行处理更容易编码。在此模式中，系统中的每个 actor 都可接收消息；执行该消息所表示的操作；然后将消息发送给其他 actor（包括它们自己）以执行复杂的操作序列。actor 之间的所有消息是异步的，这意味着发送者会在收到任何回复之前继续进行处理。因此，一个 actor 可能终生都陷入接收和处理消息的无限循环中。

CRUSH全称Controlled Replication Under Scalable Hashing，是一种数据分发算法，类似于哈希和一致性哈希。哈希的问题在于数据增长时不能动态加Bucket，一致性哈希的问题在于加Bucket时数据迁移量比较大，其他数据分发算法依赖中心的Metadata服务器来存储元数据效率较低，CRUSH则是通过计算、接受多维参数的来解决动态数据分发的场景。 数据分布算法面临了几个挑战：

1，Cassandra Cassandra集群中的节点没有主次之分，它们通过一种叫做Gossip的协议进行通信。通过Gossip协议，它们可以知道集群中有哪些节点，以及这些节点的状态如何？每一条Gossip消息上都有一个版本号，节点可以对接收到的消息进行版本比对，从而得知哪些消息是我需要更新的，哪些消息是我有而别人没有的，然后互相倾诉吐槽，确保二者得到的信息相同，这很像现实生活中的八卦（摆龙门阵）一样，一传十，十传百，最后尽人皆知。 在Cassandra启动时，会启动Gossip服务，Gossip服务启动后会启动一个任务GossipTask，这个任务会周期性地与其他节点进行通信。 2，Consul 　Consul使用gossip协议来管理成员和广播消息到集群。所有这些都是通过使用Serf库提供的。Serf使用的gossip协议基于“SWIM: Scalable Weakly-consistent Infection-style Process Group Membership Protocol”，有一些小的修改。更多关于Serf的协议细节见此文档。

Gossip是一种去中心化、容错并保证最终一致性的协议。

一、分布式系统的难点 分布式系统比起单机系统存在哪些难点呢？

1，Raft算法 raft 集群中的每个节点都可以根据集群运行的情况在三种状态间切换：follower, candidate 与 leader。leader 向 follower 同步日志，follower 只从 leader 处获取日志。在节点初始启动时，节点的 raft 状态机将处于 follower 状态并被设定一个 election timeout，如果在这一时间周期内没有收到来自 leader 的 heartbeat，节点将发起选举：节点在将自己的状态切换为 candidate 之后，向集群中其它 follower 节点发送请求，询问其是否选举自己成为 leader。当收到来自集群中过半数节点的接受投票后，节点即成为 leader，开始接收保存 client 的数据并向其它的 follower 节点同步日志。leader 节点依靠定时向 follower 发送 heartbeat 来保持其地位。任何时候如果其它 follower 在 election timeout 期间都没有收到来自 leader 的 heartbeat，同样会将自己的状态切换为 candidate 并发起选举。每成功选举一次，新 leader 的步进数都会比之前 leader 的步进数大1。

DHT(Distributed Hash Table，分布式哈希表)类似Tracker的根据种子特征码返回种子信息的网络。DHT全称叫分布式哈希表(Distributed Hash Table)，是一种分布式存储方法。在不需要服务器的情况下，每个客户端负责一个小范围的路由，并负责存储一小部分数据，从而实现整个DHT网络的寻址和存储。新版BitComet允许同时连接DHT网络和Tracker，也就是说在完全不连上Tracker服务器的情况下，也可以很好的下载，因为它可以在DHT网络中寻找下载同一文件的其他用户。 Kademlia(简称Kda)属于一种典型的结构化P2P覆盖网络(Structured P2P OverlayNetwork)，以分布式的应用层全网方式来进行信息的存储和检索是其尝试解决的主要问题。在Kademlia网络中，所有信息均以哈希表条目形式加以存储，这些条目被分散地存储在各个节点上，从而以全网方式构成一张巨大的分布式哈希表。我们可以形象地把这张哈希大表看成是一本字典：只要知道了信息索引的key，我们便可以通过Kademlia协议来查询其所对应的value信息，而不管这个value信息究竟是存储在哪一个节点之上。在eMule、BitTorrent等P2P文件交换系统中，Kademlia主要充当了文件信息检索协议这一关键角色，但Kad网络的应用并不仅限于文件交换。

一、P2P及DHT技术简介 P2P在思想上可以说是internet思想/精神/哲学非常集中的体现，共同的参与，透明的开放，平等的分享（让我想起之前学习过的，现在正在疯狂热炒的云计算的“中央集权”制度）。基于P2P技术的应用有很多，包括文件分享，即时通信，协同处理，流媒体通信等等。通过这些应用的接触，分析和理解，P2P其本质是一种新的网络传播技术，这种新的传播技术打破了传统的C/S架构，逐步地去中心化，扁平化，这或许在一定程度上应证了”世界是平的”趋势，呵呵。P2P文件分享的应用(BTs/eMules等)是P2P技术最集中的体现，我们这里的研究也是以P2P文件分享网络作为入口，P2P文件分享网络的发展大致有以下几个阶段，包含tracker服务器的网络，无任何服务器的纯DHT网络， 混合型P2P网络。DHT网络发展即有“思想/文化”上的“发展”，也有一定的商业上的需求（版权管理）。

研究表明，对于一些基分类器来说，与不均衡的数据集相比一个均衡的数据集可以提高全局的分类性能。数据层面的处理方法是处理不均衡数据分类问题的重要途径之一，它的实现方法主要分为对多数类样本的欠抽样和对少数类样本的过抽样学习两种。其主要思想是通过合理的删减或者增加一些样本来实现数据均衡的目的，进而降低数据不均衡给分类器带来的负面影响。 按照对样本数量的影响又可分为： 过抽样，即合理地增加少数类的样本 欠抽样，即合理地删减多数类样本 随机过抽样和欠抽样 随机过抽样 随机过抽样是一种按照下面的描述从少数类中速记抽样生成子集合 E 的方法。 首先在少数类 Smin 集合中随机选中一些少数类样本 然后通过复制所选样本生成样本集合 E 将它们添加到 Smin 中来扩大原始数据集从而得到新的少数类集合 Smin−new 用这样方法，Smin 中的总样本数增加了 |E| 个新样本，且 Smin−new 的类分布均衡度进行相应的调整，如此操作可以改变类分布平衡度从而达到所需水平。 欠抽样 欠抽样技术是将数据从原始数据集中移除。 首先我们从 Smaj 中随机地选取一些多数类样本 E 将这些样本从 Smaj 中移除，就有 |Smaj−new|=|Smaj|−|E| 缺陷 初看，过抽样和欠抽样技术在功能上似乎是等价的，因为它们都能改变原始数据集的样本容量且能够获得一个相同比例的平衡。 但是，这个共同点只是表面现象，这是因为这两种方法都将会产生不同的降低分类器学习能力的负面效果。 对于欠抽样算法，将多数类样本删除有可能会导致分类器丢失有关多数类的重要信息。 对于过抽样算法，虽然只是简单地将复制后的数据添加到原始数据集中，且某些样本的多个实例都是“并列的”，但这样也可能会导致分类器学习出现过拟合现象，对于同一个样本的多个复本产生多个规则条例，这就使得规则过于具体化；虽然在这种情况下，分类器的训练精度会很高，但在位置样本的分类性能就会非常不理想。 informed 欠抽样 两个 informed 欠抽样算法：EasyEnsemble 和 BalanceCascade 算法，这两种方法克服了传统随机欠抽样方法导致的信息缺失的问题，且表现出较好的不均衡数据分类性能。 EasyEnsemble 和 BalanceCascade 算法介绍

1. EasyEnsemble 核心思想是： 首先通过从多数类中独立随机抽取出若干子集 将每个子集与少数类数据联合起来训练生成多个基分类器 最终将这些基分类器组合形成一个集成学习系统 EasyEnsemble 算法被认为是非监督学习算法，因此它每次都独立利用可放回随机抽样机制来提取多数类样本
2. BalanceCascade 核心思想是： 使用之前已形成的集成分类器来为下一次训练选择多类样本 然后再进行欠抽样 最近邻规则（ENN） 因为随机欠抽样方法未考虑样本的分布情况，采样具有很大的随机性，可能会删除重要的多数类样本信息。针对以上的不足，Wilson 等人提出了一种最近邻规则(edited nearest neighbor: ENN)。 基本思想：删除那些类别与其最近的三个近邻样本中的两个或两个以上的样本类别不同的样本 缺点：因为大多数的多数类样本的样本附近都是多数类，所以该方法所能删除的多数类样本十分有限。 领域清理规则 (NCL) Laur Ikkala J 等人在 ENN 的基础行提出了 领域清理规则 (neighborhod cleaning rule: NCL)。该算法的整体流程图如下所示：

KNN和K-Means的区别 KNN

我们把两组样本近似线性数据的距离称为相关系数。相关系数是衡量相似度的主要指标之一。

二分图的概念 二分图又称作二部图，是图论中的一种特殊模型。 设G=(V, E)是一个无向图。如果顶点集V可分割为两个互不相交的子集X和Y，并且图中每条边连接的两个顶点一个在X中，另一个在Y中，则称图G为二分图。

什么是二分图 若图G的结点集V(G)可以分成两个非空子集 V1和V2，并且图G的任意边xy关联的两个结点 x、y分别属于这两个子集，则图G是二分图。 所有的树都是二分图。从树中任取一个结点为树根，着上白色，然后将根的所有孩子着上黑色，将下一层再着白色，继续此过程直到所有结点都着色。 用着色法或标记法可以检测一个给定的图是不是十分图。 偶数个结点的圈是二分图，而奇数个结点的圈不是二分图。所以如果图中含有奇圈，就不是二分图。其实这是一个定理： 图G是二分图当且仅当图G不含奇圈。

gossip 是一种弱一致算法，也就是最终一致性算法。 特点： 1，去中心化，集群中各个节点都是对等的。 2，无法保证在某个时刻所有节点状态一致。 3，比较适合小数据量的同步。失败检测、路由同步、Pub/Sub、动态负载均衡

给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。 极大匹配(Maximal Matching)是指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。最大匹配(maximum matching)是所有极大匹配当中边数最大的一个匹配。选择这样的边数最大的子集称为图的最大匹配问题。 如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。 求二分图匹配可以用最大流(Maximal Flow)或者匈牙利算法(Hungarian Algorithm)

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。简而言之，就是顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属于这两个互不相交的子集，两个子集内的顶点不相邻。图中U和V构造的点集所形成的循环圈不为奇数，所以是二分图。 无向图G为二分图的充分必要条件是，G至少有两个顶点，且其所有回路的长度均为偶数。 证先证必要性。 设G为二分图<X，E，Y>。由于X，Y非空，故G至少有两个顶点。若C为G中任一回路，令 C = (v0,v 1,v2，…，v l-1,v l = v0) 其中诸vi (i = 0,1，…，l）必定相间出现于X及Y中，不妨设 {v0,v2,v4，…，v l = v0}属于 X {v1,v3,v5，…，v l-1}属于 Y 因此l必为偶数，从而C中有偶数条边。 再证充分性。 设G的所有回路具有偶数长度，并设G为连通图（不失一般性，若G不连通，则可对G的各连通分支作下述讨论）。 令G的顶点集为V，边集为E，现构作X，Y，使<X，E，Y> = G。取v0属于V，置 X = {v | v= v0或v到v0有偶数长度的通路} Y = V-X X显然非空。现需证Y非空，且没有任何边的两个端点都在X中或都在Y中。 由于|V|≥2并且G为一连通图，因此v0必定有相邻顶点，设为v1，那么v1属于Y；故Y不空。 设有边（u,v），使u属于X，v属于X。那么，v0到u有偶数长度的通路，或u = v0；v0到v有偶数长度的通路，或v = v0。无论何种情况，均有一条从v0到v0的奇数长度的闭路径，因而有从v0到v0的奇数长度的回路（因从闭路径上可能删去的回路长度总为偶数），与题设矛盾。故不可能有边（u,v）使u,v均在X中。 “没有任何边的两个端点全在Y中”的证明可仿上进行，请读者思考 [2] 。 最大匹配编辑 求二分图最大匹配可以用最大流或者匈牙利算法。 最大匹配 给定一个二分图G，在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配. 选择这样的边数最大的子集称为图的最大匹配问题（maximal matching problem) 如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。 算法 求最大匹配的一种显而易见的算法是:先找出全部匹配，然后保留匹配数最多的。但是这个算法的复杂度为边数的指数级函数。因此，需要寻求一种更加高效的算法。 增广路的定义（也称增广轨或交错轨）： 若P是图G中一条连通两个未匹配顶点的路径，并且属M的边和不属M的边（即已匹配和待匹配的边）在P上交替出现，则称P为相对于M的一条增广路径. 由增广路的定义可以推出下述三个结论： 1-P的路径长度必定为奇数，第一条边和最后一条边都不属于M. 2-P经过取反操作可以得到一个更大的匹配M’. 3-M为G的最大匹配当且仅当不存在相对于M的增广路径. 匈牙利算法 用增广路求最大匹配（称作匈牙利算法，匈牙利数学家Edmonds于1965年提出） 算法轮廓： ⑴置M为空 ⑵找出一条增广路径P，通过取反操作获得更大的匹配M’代替M ⑶重复⑵操作直到找不出增广路径为止 g:array[1..maxn,1..maxm]of boolean; y:array[1..maxm]of boolean; link:array[1..maxm]of longint; function find(v:longint):boolean; var i:longint; begin for i:=1 to m do if g[v,i] and (not y[ i ]) then begin y[ i ]:=true; if (link[ i ]=0)or find(link[ i ]) then begin link[ i ]:=v; find:=true; exit; end; end; find:=false; end; begin //read the graph into array g[][] for i:=1 to n do begin fillchar(y,sizeof(y),0); if find(i) then inc(ans); end; 其中n,m分别为2部图两边节点的个数，两边的节点分别用1..n,1..m编号 g[x][y]=true表示x,y两个点之间有边相连 link[y]记录的是当前与y节点相连的x节点 y记录的是y中的i节点是否被访问过. 算法的思路是不停的找增广轨，并增加匹配的个数，增广轨顾名思义是指一条可以使匹配数变多的路径，在匹配问题中，增广轨的表现形式是一条”交错轨”,也就是说这条由图的边组成的路径，它的第一条边是目前还没有参与匹配的，第二条边参与了匹配，第三条边没有..最后一条边没有参与匹配，并且始点和终点还没有被选择过.这样交错进行，显然他有奇数条边.那么对于这样一条路径，我们可以将第一条边改为已匹配，第二条边改为未匹配…以此类推.也就是将所有的边进行”反色”,容易发现这样修改以后，匹配仍然是合法的，但是匹配数增加了一对.另外，单独的一条连接两个未匹配点的边显然也是交错轨.可以证明，当不能再找到增广轨时，就得到了一个最大匹配.这也就是匈牙利算法的思路. 代码中find(i）就是寻找有没有从x点i开始的增广轨，如果有就进行上述操作，代码是递归的，所以看起来不是很显然，画个图试试就很清楚了。 性质编辑 二分图中，点覆盖数是匹配数。 　　（1）二分图的最大匹配数等于最小覆盖数，即求最少的点使得每条边都至少和其中的一个点相关联，很显然直接取最大匹配的一段节点即可。 　　（2）二分图的独立数等于顶点数减去最大匹配数，很显然的把最大匹配两端的点都从顶点集中去掉这个时候剩余的点是独立集，这是|V|-2*|M|，同时必然可以从每条匹配边的两端取一个点加入独立集并且保持其独立集性质。 　　（3）DAG的最小路径覆盖，将每个点拆点后作最大匹配，结果为n-m，求具体路径的时候顺着匹配边走就可以，匹配边i→j’,j→k’,k→l’….构成一条有向路径。 （4）最大匹配数=左边匹配点+右边未匹配点。因为在最大匹配集中的任意一条边，如果他的左边没标记，右边被标记了，那么我们就可找到一条新的增广路，所以每一条边都至少被一个点覆盖。 （5）最小边覆盖=图中点的个数-最大匹配数=最大独立集。 判定编辑 二分图是这样一个图： 有两顶点集且图中每条边的的两个顶点分别位于两个顶点集中，每个顶点集中没有边直接相连接！ 无向图G为二分图的充分必要条件是，G至少有两个顶点,且其所有回路的长度均为偶数。 判断二分图的常见方法是染色法： 开始对任意一未染色的顶点染色，之后判断其相邻的顶点中，若未染色则将其染上和相邻顶点不同的颜色， 若已经染色且颜色和相邻顶点的颜色相同则说明不是二分图，若颜色不同则继续判断，bfs和dfs可以搞定！ 易知：任何无回路的的图均是二分图 [3] 。 C语言实例 //其中n,m分别为2部图两边节点的个数，两边的节点分别用0..n-1,0..m-1编号 bool g[n][m];//g[x][y]表示x,y两个点之间有边相连 bool y[m];//y[i]记录的是y中的i节点是否被访问过. int link[m];//link[y]记录的是当前与y节点相连的x节点 bool find(int v) { int i; for(i=0;i<m;i++) { if(g[v][i]&&!y[i]) { y[i]=true; if(link[i]==-1||find(link[i])) { link[i]=v; return true; } } } return false; } int main() { //read the graph int array g[][] memset(link,-1,sizeof(link)); for(i=0;i<n;i++) { memset(y,0,sizeof(y)); if(find(i)) ans++; } return 0; }

若P是图G中一条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径（举例来说，有A、B集合，增广路由A中一个点通向B中一个点，再由B中这个点通向A中一个点……交替进行）。 由增广路的定义可以推出下述五个结论： 1－P的路径长度必定为奇数，第一条边和最后一条边都不属于M。 2－不断寻找增广路可以得到一个更大的匹配M’，直到找不到更多的增广路。 3－M为G的最大匹配当且仅当不存在M的增广路径。 4－最大匹配数M+最大独立数N=总的结点数 5 – 二分图的最小路径覆盖数 = 原图点数 - 最大匹配数 增广路主要应用于匈牙利算法中，用于求二分图最大匹配。

如果二分图的每条边都有一个权（可以是负数），要求一种完备匹配方案，使得所有匹配边的权和最大，记做最佳完美匹配。（特殊的，当所有边的权为1时，就是最大完备匹配问题） 我们使用KM算法解决该问题。

二分图：简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交集 和 ，使得每一条边都分别连接 中的顶点。如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。 最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。 完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。 交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替 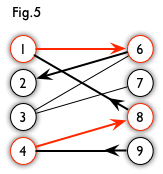增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。 增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。 我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的。在给出匈牙利算法 DFS 和 BFS 版本的代码之前，先讲一下匈牙利树。 匈牙利树一般由 BFS 构造（类似于 BFS 树）。从一个未匹配点出发运行 BFS（唯一的限制是，必须走交替路），直到不能再扩展为止。 // 由于时间紧凑，代码摘自http://dsqiu.iteye.com/blog/1689505 #define maxn 10//表示x集合和y集合中顶点的最大个数！
int nx,ny;//x集合和y集合中顶点的个数
int edge[maxn][maxn];//edge[i][j]为1表示ij可以匹配
int cx[maxn],cy[maxn];//用来记录x集合中匹配的y元素是哪个！
int visited[maxn];//用来记录该顶点是否被访问过！
int path(int u) {
int v;
for(v=0;v<ny;v++)
{
if(edge[u][v]&&!visited[v])
{
visited[v]=1;
if(cy[v]==-1||path(cy[v]))//如果y集合中的v元素没有匹配或者是v已经匹配，但是从cy[v]中能够找到一条增广路
{
cx[u]=v; //找到增广路，修改匹配M
cy[v]=u;
return 1;
}
}
}
return 0;
}
int maxmatch()
{
int res=0;
memset(cx,0xff,sizeof(cx));//初始值为-1表示两个集合中都没有匹配的元素！
memset(cy,0xff,sizeof(cy));
for(int i=0;i<=nx;i++)
{
if(cx[i]==-1) //还没被匹配，执行内部代码
{
memset(visited,0,sizeof(visitited)); //重置标记为为访问
res+=path(i); //以 i 为起点开始查找增广路，返回true ，匹配数+1
}
}
return res;
}

基本的网络流模型，最基础的最大流求法，即bfs找增广路法，也就是EK法，全名是Edmond-Karp，其实我倒是觉得记一下算法的全名和来历可以不时的拿出来装一装。