https://segmentfault.com/a/1190000022367093
2-3-4树和普通红黑树
某些教程不区分普通红黑树和左倾红黑树的区别，直接将左倾红黑树拿来教学，并且称其为红黑树，因为左倾红黑树与普通的红黑树相比，实现起来较为简单，容易教学。在这里，我们区分开左倾红黑树和普通红黑树。

红黑树是一种近似平衡的二叉查找树，从2-3树或2-3-4树衍生而来。通过对二叉树节点进行染色，染色为红或黑节点，来模仿2-3树或2-3-4树的3节点和4节点，从而让树的高度减小。2-3-4树对照实现的红黑树是普通的红黑树，而2-3树对照实现的红黑树是一种变种，称为左倾红黑树，其更容易实现。

使用平衡树数据结构，可以提高查找元素的速度，我们在本章介绍2-3-4树，再用二叉树形式来实现2-3-4树，也就是普通的红黑树。

一、2-3-4 树
1.1. 2-3-4 树介绍
2-3-4树是一棵严格自平衡的多路查找树，又称4阶的B树(注：B为Balance平衡的意思)

它不是一棵二叉树，是一棵四叉树。具有以下特征：

内部节点要么有1个数据元素和2个孩子，要么有2个数据元素和3个孩子，要么有3个数据元素和4个孩子，叶子节点没有孩子，但有1，2或3个数据元素。
所有叶子节点到根节点的长度一致。这个特征保证了完全平衡，非常完美的平衡。
每个节点的数据元素保持从小到大排序，两个数据元素之间的子树的所有值大小介于两个数据元素之间。
因为2-3-4树的第二个特征，它是一棵完美平衡的树，非常完美，除了叶子节点，其他的节点都没有空儿子，所以树的高度非常的小。

如果一个内部节点拥有一个数据元素、两个子节点，则此节点为2节点。如果一个内部节点拥有两个数据元素、三个子节点，则此节点为3节点。如果一个内部节点拥有三个数据元素、四个子节点，则此节点为4节点。

可以说，所有平衡树的核心都在于插入和删除逻辑，我们主要分析这两个操作。

1.2. 2-3-4 树插入元素
在插入元素时，需要先找到插入的位置，使用二分查找从上自下查找树节点。

找到插入位置时，将元素插入该位置，然后进行调整，使得满足2-3-4树的特征。主要有三种情况：

插入元素到一个2节点或3节点，直接插入即可，这样节点变成3节点或4节点。
插入元素到一个4节点，该4节点的父亲不是一个4节点，将4节点的中间元素提到父节点，原4节点变成两个2节点，再将元素插入到其中一个2节点。
插入元素到一个4节点，该4节点的父亲是一个4节点，也是将4节点的中间元素提到父节点，原4节点变成两个2节点，再将元素插入到其中一个2节点。当中间元素提到父节点时，父节点也是4节点，可以递归向上操作。
核心在于往4节点插入元素时，需要将4节点中间元素提升，4节点变为两个2节点后，再插入元素，如图：

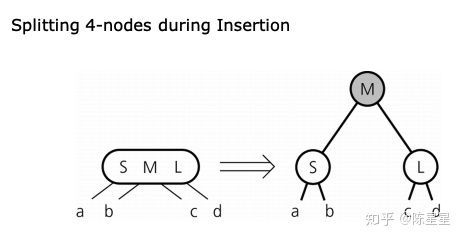
下面演示插入元素到一个4节点：

与其他二叉查找树由上而下生长不同，2-3-4树是从下至上的生长。

2-3-4树因为节点元素数量的增加，情况变得更复杂，下面是插入元素到一个4节点，而4节点的父节点是3节点的三种情况
其他情况可以参考2-3树和左倾红黑树一章，非常相似，在此不再赘述。

1.3. 2-3-4 树删除元素
删除操作就复杂得多了，请耐心阅读理解，和2-3树删除元素类似。

2-3-4树的特征注定它是一棵非常完美平衡的四叉树，其所有子树也都是完美平衡，所以2-3-4树的某节点的儿子，要么都是空儿子，要么都不是空儿子。比如2-3-4树的某个节点A有两个儿子B和C，儿子B和C要么都没有孩子，要么孩子都是满的，不然2-3-4树所有叶子节点到根节点的长度一致这个特征就被破坏了。

基于上面的现实，我们来分析删除的不同情况，删除中间节点和叶子节点。

情况1：删除中间节点

删除的是非叶子节点，该节点一定是有两棵，三棵或者四棵子树的，那么从子树中找到其最小后继节点，该节点是叶子节点，用该节点替换被删除的非叶子节点，然后再删除这个叶子节点，进入情况2。

如何找到最小后继节点，当有两棵子树时，那么从右子树一直往左下方找，如果有三棵子树，被删除节点在左边，那么从中子树一直往左下方找，否则从右子树一直往左下方找。如果有四棵子树，那么往被删除节点右边的子树，一直往左下方找。

情况2：删除叶子节点

删除的是叶子节点，这时叶子节点如果是4节点，直接变为3节点，如果是3节点，那么直接变为2节点即可，不影响平衡。但是，如果叶子节点是2节点，那么删除后，其父节点将会缺失一个儿子，破坏了满孩子的2-3-4树特征，需要进行调整后才能删除。

针对情况2，删除一个2节点的叶子节点，会导致父节点缺失一个儿子，破坏了2-3-4树的特征，我们可以进行调整变换，主要有两种调整：

重新分布：尝试从兄弟节点那里借值，然后重新调整节点。
合并：如果兄弟借不到值，合并节点（与父亲的元素）。
如果被删除的叶子节点有兄弟是3节点或4节点，可以向最近的兄弟借值，然后重新分布，这样叶子节点就不再是2节点了，删除元素后也不会破坏平衡。如图：

与兄弟借值，兄弟必须有多余的元素可以借，借的过程中需要和父节点元素重新分布位置，确保符合元素大小排序的正确。

如果被删除的叶子节点，兄弟都是2节点，而父亲是3节点或4节点，那么将父亲的一个元素拉下来进行合并（当父节点是3节点时，父亲元素与被删除节点合并成3节点，当父节点是4节点时，被删除节点和其最近的兄弟，以及父亲的一个元素合并成一个4节点），父亲变为2节点或3节点，这时叶子节点就不再是2节点了，删除元素后也不会破坏平衡。如图：

有一种最特殊的情况，也就是被删除的叶子节点，兄弟都是2节点，父亲也是2节点，这种情况没法向兄弟借，也没法和父亲合并，与父亲合并后父亲就变空了。幸运的是，这种特殊情况只会发生在根节点是其父节点的情况，如图：

因为2-3-4树的性质，除了根节点，其他节点不可能出现其本身和儿子都是2节点。

2-3-4树的实现将会放在B树章节，我们将会实现其二叉树形式的普通红黑树结构。

二、 普通红黑树
2.1. 普通红黑树介绍
普通红黑树可以由2-3-4树的二叉树形式来实现。

其定义为：

根节点的链接是黑色的。
每个红色节点都必须有两个黑色子节点。
任意一个节点到达叶子节点的所有路径，经过的黑链接数量相同，也就是该树是完美黑色平衡的。比如，某一个节点，它可以到达5个叶子节点，那么这5条路径上的黑链接数量一样。
普通红黑树与其变种：左倾红黑树的区别是，它允许右倾的红色节点，不再限制左倾，但仍然不能有连续的两个左倾红色链接。

每一棵2-3-4树可以对应多棵普通红黑树，如图：

区别：2-3树与左倾红黑树则是一一对应，而2-3-4树可以对应多棵普通红黑树，是因为它允许了红链接右倾。
https://goa.lenggirl.com/
https://segmentfault.com/a/1190000022289012
https://segmentfault.com/a/1190000022288980