实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

示例 1:
输入: haystack = “hello”, needle = “ll”
输出: 2

示例 2:
输入: haystack = “aaaaa”, needle = “bba”
输出: -1
说明:

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符

解题思路：

1，用暴力解法，时间复杂度是O（mn）

2，使用kmp算法是用空间换时间，用O（m）的空间可以获得O（m＋n）的时间复杂度

3，next数组的作用：记录当前的后缀字串与前缀子串最大匹配长度。已经比较过的地方可以不用比较

4，思想和dp很像，但是空间复杂度O（m）比dp O（mn）低

代码实现

func strStr(haystack string, needle string) int {
if haystack==needle || needle==””{
return 0
}
if len(needle)==0{
return -1
}
next:=getNext(needle)
m:=0
for i:=0;i<len(haystack);i++{
for m>0 && haystack[i]!=needle[m]{
m=next[m-1]
}
if haystack[i]==needle[m]{
m++
if m==len(needle){
return i-m+1
}
}
}
return -1
}

func getNext(needle string)[]int{
next:=make([]int,len(needle))
i:=0 //代表前一个字符前后缀能匹配的最大长度
for j:=1;j<len(needle);j++{//next[0] = 0，因此从1开始
for i>0 && needle[i]!=needle[j]{ //递归直到q为0（没有匹配的前缀）或者当前字符与q相等时（不断“递归”查前缀匹配的前一个位置q）
i=next[i-1] //如果不相等，如“acad”,j=3,i=1,则i变成nexti-1
}
if needle[j]==needle[i]{
i++
}
next[j]=i
}
return next
}

相似的查找算法有 KMP，BM，Horspool, Sunday 算法。
https://www.bilibili.com/video/av3246487?from=search&seid=2862258922629755080

KMP的主要思想是利用字符串自身的前缀后缀的对称性，来构建next数组，从而实现用接近O(N)的时间复杂度完成字符串的匹配

对于一个字符串str，next[j] = k 表示满足str[0…k-1] = str[j-k…j-1]的最大的k，即对于子串str[0…j-1]，前k个字母等于后k个字母

现在求解str的next数组：

初始化：next[0] = -1

那么在知道了next[j]的情况下，如何递推地求出next[j+1]呢？分两种情况（令k=next[j]）：

　　1、如果str[j]==str[k]，则next[j+1] = k+1

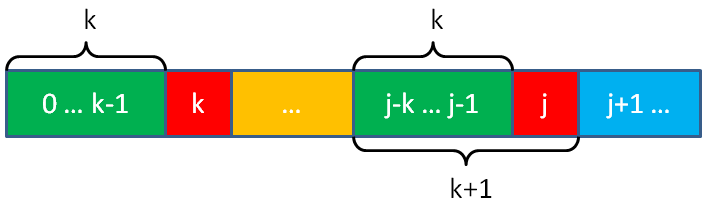
　　如下图所示，对于str[0…j-1]，前k个字母等于后k个字母（两个绿色部分相等），然后str[k]刚好是前k个字母的下一个字母（第一个红色）

　　如果str[j]==str[k]，说明对于str[0…j]，前k+1个字母等于后k+1个字母（绿色+红色=绿色+红色），即等于next[j]+1（绿色长度为k，红色长度为1）
　　
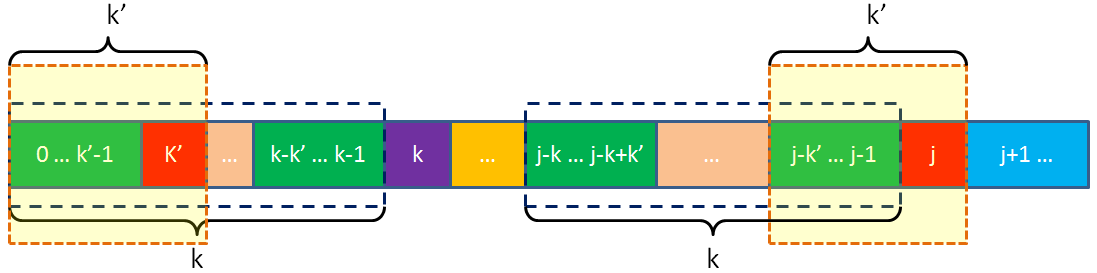
　　2、如果str[j]!=str[k]，则k=next[k]，然后继续循环（回到1），直到k=-1

　　因为str[j]!=str[k]（下图中紫色和红色不相等），所以前k+1个字母不再等于后k+1个字母了

　　但是由于前k个字母还是等于后k个字母（图中两个黑色虚线框住部分），所以对于任意的k’<k，str[k-k’…k-1]=str[j-k’…j-1]（图中第二个和最后一个绿色相等）

　　而next[k]表示str[0…k-1]内部的对称情况，所以令k’=next[k]，则对于str[0…k-1]，前k’个字母等于后k’个字母（图中第一个和第二个绿色相等）

　　由于图中第二个绿色始终=第四个绿色，所以第一个绿色等于第四个绿色

　　因此将k=next[l]继续带入循环，回到判断1：

　　　　如果str[k’]=str[j]，则满足前k’+1个字母等于后k’+1个字母（两个浅黄色区域相等），所以next[j+1] = k’+1；

　　　　否则，继续k’=next[k’]继续循环，直到k’=-1说明已经到达第一个元素，不能继续划分，next[j+1]=0