KM(Kuhn and Munkres)算法
如果二分图的每条边都有一个权(可以是负数),要求一种完备匹配方案,使得所有匹配边的权和最大,记做最佳完美匹配。(特殊的,当所有边的权为1时,就是最大完备匹配问题)
我们使用KM算法解决该问题。
KM(Kuhn and Munkres)算法,是对匈牙利算法的一种贪心扩展,如果对匈牙利算法还不够明白,建议先重新回顾一下匈牙利算法。
KM是对匈牙利算法的一种贪心扩展,这种贪心不是对边的权值的贪心,算法发明者引入了一些新的概念,从而完成了这种扩展。
可行顶标
对于原图中的任意一个结点,给定一个函数L(node)求出结点的顶标值。我们用数组lx(x)记录集合X中的结点顶标值,用数组ly(y)记录集合Y中的结点顶标值。
并且,对于原图中任意一条边edge(x,y),都满足
lx(x)+ly(y)>=weight(x,y)
相等子图
相等子图是原图的一个生成子图(生成子图即包含原图的所有结点,但是不包含所有的边),并且该生成子图中只包含满足
lx(x)+ly(y)=weight(x,y)
的边,这样的边我们称之为可行边。
算法原理
定理:如果原图的一个相等子图中包含完备匹配,那么这个匹配就是原图的最佳二分图匹配。
证明 :由于算法中一直保持顶标的可行性,所以任意一个匹配的权值之和肯定小于等于所有结点的顶标之和,则相等子图中的完备匹配肯定是最优匹配。
这就是为什么我们要引入可行顶标和相等子图的概念。
上面的证明可能太过抽象,我们结合图示更直观的表述。
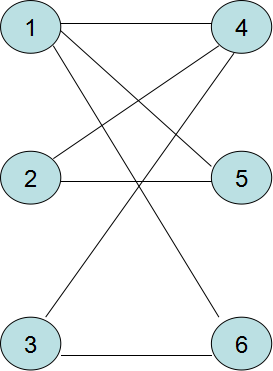
该图表示原图,且X=1,2,3,Y=4,5,6,给出权值
weight(1,4)=5
weight(1,5)=10
weight(1,6)=15
weight(2,4)=5
weight(2,5)=10
weight(3,4)=10
weight(3,6)=20
对于原图的任意一个匹配M
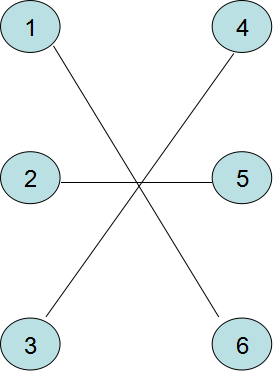
那么对于
edge(1,6)weight(1,6)=15
edge(2,5)weight(2,5)=10
edge(3,4)weight(3,4)=10
都满足
lx(x)+ly(y)>=weight(x,y)
所以
∑i=1xi∈Xlx(xi)+∑i=1yi∈Yly(yi)=K>=∑weight(xi,yi)
可以看出,一个匹配中的边权之和最大为K。
那么很显然,当一个匹配G∗的边权之和恰好为K时,那么G∗就是二分图的最佳完美匹配。
如果对于每一条边edge(xi,yi)都满足
lx(xi)+ly(yi)==weight(xi,yi)
那么
∑i=1xi∈Xlx(xi)+∑i=1yi∈Yly(yi)=K=∑weight(xi,yi)
相等子图的完备匹配(完美匹配)即满足上述条件(因为相等子图的每条边都是可行边,可行边满足lx(xi)+ly(yi)=weight(xi,yi))所以当相等子图有完备匹配的时候,原图有最佳完美匹配。
KM的算法流程
流程
Kuhn-Munkras算法(即KM算法)流程:
初始化可行顶标的值 (设定lx,ly的初始值)
用匈牙利算法寻找相等子图的完备匹配
若未找到增广路则修改可行顶标的值
重复(2)(3)直到找到相等子图的完备匹配为止
KM算法的核心部分即控制修改可行顶标的策略使得最终可到达一个完美匹配。
初始时,设定lx[xi]为和xi相关联的edge(xi,yj)的最大权值,ly[yj]=0,满足公式lx[xi]+ly[yj]>=weight(xi,yj)
当相等子图中不包含完备匹配的时候(也就是说还有增广路),就适当修改顶标。直到找到完备匹配为止。(整个过程在匈牙利算法中执行)
现在我们的问题是,遵循什么样的原则去修改顶标的值?
对于正在增广的增广路径上属于集合X的所有点减去一个常数delta,属于集合Y的所有点加上一个常数delta。
为什么要这样做呢,我们来分析一下:
对于图中任意一条边edge(i,j) (其中xi∈X,xj∈Y)权值为weight(i,j)
如果i和j都属于增广路,那么lx[i]−delta+ly[j]−+delta=lx[i]+ly[j]值不变,也就说edge(i,j)可行性不变,原来是相等子图的边就还是,原来不是仍然不是
如果i属于增广路,j不属于增广路,那么lx[i]−delta+ly[j]的值减小,也就是原来这条边不在相等子图中(否则j就会被遍历到了),现在可能就会加入到相等子图。
如果i不属于增广路,j属于增广路,那么lx[i]+ly[j]+delta的值增大,也就是说原来这条边不在相等子图中(否则j就会被遍历到了),现在还不可能加入到相等子图
如果i,j都不属于增广路,那么lx[i]和ly[j]都不会加减常数delta值不变,可行性不变
这 样,在进行了这一步修改操作后,图中原来的可行边仍可行,而原来不可行的边现在则可能变为可行边。那么delta的值应取多少?
观察上述四种情况,只有第二类边(xi∈X,yj∈Y)的可行性经过修改可以改变。
因为对于每条边都要满足lx(i)+ly(j)>=weight(i,j),这一性质绝对不可以改变,所以取第二种情况的 lx[i]+ly[j]−weight(i,j)的最小值作为delta。
证明 :
delta=Min(lx[i]+ly[j]−weight(i,j))=lx[i]+ly[j]−Max(weight(i,j))
第二类边 :
lx[i]−delta+ly[j]=lx[i]−lx[i]−ly[i]+Max(weight(i,j))+ly[j]=Max(weight)>=weight(i,j)
成立
下面我们重新回顾一下整个KM算法的流程 :
可行顶标:每个点有一个标号,记(xi∈X,yj∈Y)。如果对于图中的任意边edge(i,j)都有lx[i]+ly[j]>=weight(i,j),则这一顶标是可行的。特别地,对于lx[i]+ly[j]=weight(i,j),称为可行边(也就是相等子图里的边)
KM 算法的核心思想就是通过修改某些点的标号(但要满足点标始终是可行的),不断增加图中的可行边总数,直到图中存在仅由可行边组成的完全匹配为止,此时这个 匹配一定是最佳的(证明上文已经给出)
初始化:lx[i]=Max(edge(i,j)),xi∈X,edge(i,j)∈E,ly[j]=0。这个初始顶标显然是可行的,并且,与任意一个X方点关联的边中至少有一条可行边
从每个X方点开始DFS增广。DFS增广的过程与最大匹配的Hungary算法基本相同,只是要注意两点:一是只找可行边,二是要把搜索过程中遍历到的X方点全部记下来,以便进行后面的修改
增广的结果有两种:若成功(找到了增广路),则该点增广完成,进入下一个点的增广。若失败(没有找到增广路),则需要改变一些点的标号,使得图中可行边的 数量增加。
修改后,继续对这个X方点DFS增广,若还失败则继续修改,直到成功为止
伪代码
bool findpath(x)
{
visx[x] = true;
for(int y = 1 ; y <= ny ; ++y)
{
if(!visy[y] && lx[x] + ly[y] == weight(x,y)) //y不在交错路中且edge(x,y)必须在相等子图中
{
visy[y] = true;
if(match[y] == -1 || findpath(match[y]))//如果y还为匹配或者从y的match还能另外找到一条匹配边
{
match[y] = x;
return true;
}
}
}
return false;
}
void KM()
{
for(int x = 1 ; x <= nx ; ++x)
{
while(true)
{
memset(visx,false,sizeof(visx));//访问过X中的标记
memset(visy,false,sizeof(visy));//访问过Y中的标记
if(findpath(x))//找到了增广路,跳出继续寻找下一个
break;
else
{
for(int i = 1 ; i <= nx ; ++i)
{
if(visx[i])//i在交错路中
{
for(int j = 1 ; j <= ny ; ++j)
{
if(visy[j])//j不在交错路中,对应第二类边
delta = Min(delta,lx[x] + ly[y] - weight(i,j))
}
}
}
for(int i = 1 ; i <= nx ; ++i)//增广路中xi - delta
if(visx[i])
lx[i] -= delta;
for(int j = 1 ; j <= ny ; ++j)//增广路中yj + delta
if(visy[j])
ly[j] += delta;
}
} } 这种形式的KM算法的时间复杂度为O(n4) KM算法的优化 KM算法可以优化到O(n3) 一个优化是对Y顶点引入松弛函数slack,slack[j]保存跟当前节点j相连的节点i的lx[i]+ly[j]−weight(i,j)的最小值,于是求delta时只需O(n)枚举不在交错树中的Y顶点的最小slack值即可。
松弛值可以在匈牙利算法检查相等子树边失败时进行更新,同时在修改标号后也要更新,具体参考代码实现。
(hdu 2255 模板)
/*
实际上,O(n^4)的KM算法表现不俗,使用O(n^3)并不会很大的提高KM的运行效率
需要在O(1)的时间找到任意一条边,使用邻接矩阵存储更为方便
*/
#include
#include
const int maxn = 305;
const int INF = 0x3f3f3f3f;
int match[maxn],lx[maxn],ly[maxn],slack[maxn];
int G[maxn][maxn];
bool visx[maxn],visy[maxn];
int n,nx,ny,ans;
bool findpath(int x)
{
int tempDelta;
visx[x] = true;
for(int y = 0 ; y < ny ; ++y){
if(visy[y]) continue;
tempDelta = lx[x] + ly[y] - G[x][y];
if(tempDelta == 0){//(x,y)在相等子图中
visy[y] = true;
if(match[y] == -1 || findpath(match[y])){
match[y] = x;
return true;
}
}
else if(slack[y] > tempDelta)
slack[y] = tempDelta;//(x,y)不在相等子图中且y不在交错树中
}
return false; } void KM() {
for(int x = 0 ; x < nx ; ++x){
for(int j = 0 ; j < ny ; ++j) slack[j] = INF;//这里不要忘了,每次换新的x结点都要初始化slack
while(true){
memset(visx,false,sizeof(visx));
memset(visy,false,sizeof(visy));//这两个初始化必须放在这里,因此每次findpath()都要更新
if(findpath(x)) break;
else{
int delta = INF;
for(int j = 0 ; j < ny ; ++j)//因为dfs(x)失败了所以x一定在交错树中,y不在交错树中,第二类边
if(!visy[j] && delta > slack[j])
delta = slack[j];
for(int i = 0 ; i < nx ; ++i)
if(visx[i]) lx[i] -= delta;
for(int j = 0 ; j < ny ; ++j){
if(visy[j])
ly[j] += delta;
else
slack[j] -= delta;
//修改顶标后,要把所有的slack值都减去delta
//这是因为lx[i] 减小了delta
//slack[j] = min(lx[i] + ly[j] -w[i][j]) --j不属于交错树--也需要减少delta,第二类边
}
}
}
} } void solve() {
memset(match,-1,sizeof(match));
memset(ly,0,sizeof(ly));
for(int i = 0 ; i < nx ; ++i){
lx[i] = -INF;
for(int j = 0 ; j < ny ; ++j)
if(lx[i] < G[i][j])
lx[i] = G[i][j];
}
KM();
}
int main()
{
while(scanf(“%d”,&n) != EOF){
nx = ny = n;
for(int i = 0 ; i < nx ; ++i)
for(int j = 0 ; j < ny ; ++j)
scanf(“%d”,&G[i][j]);
solve();
int ans = 0;
for(int i = 0 ; i < ny ; ++i)
if(match[i] != -1)
ans += G[match[i]][i];
printf(“%d\n”,ans);
}
return 0;
}
上面讲的都是求最大权的完备匹配,如果要求最小权完备匹配,只需在调用km算法前把所有权值都取反,然后再调用km算法,然后把km算法得到的结果再取反即为最小权值。
[二分图带权匹配与最佳匹配]
什么是二分图的带权匹配?二分图的带权匹配就是求出一个匹配集合,使得集合中边的权值之和最大或最小。而二分图的最佳匹配则一定为完备匹配,在此基础上,才要求匹配的边权值之和最大或最小。二分图的带权匹配与最佳匹配不等价,也不互相包含。
我们可以使用KM算法实现求二分图的最佳匹配。方法我不再赘述,可以参考tianyi的讲解。KM算法可以实现为O(N^3)。
[KM算法的几种转化]
KM算法是求最大权完备匹配,如果要求最小权完备匹配怎么办?方法很简单,只需将所有的边权值取其相反数,求最大权完备匹配,匹配的值再取相反数即可。
KM算法的运行要求是必须存在一个完备匹配,如果求一个最大权匹配(不一定完备)该如何办?依然很简单,把不存在的边权值赋为0。
KM算法求得的最大权匹配是边权值和最大,如果我想要边权之积最大,又怎样转化?还是不难办到,每条边权取自然对数,然后求最大和权匹配,求得的结果a再算出e^a就是最大积匹配。至于精度问题则没有更好的办法了。
[求最小(大)权匹配的费用流建模方法]
求最小(大)权匹配,可以用最小(大)费用最大流的方法。和二分图最大匹配的构图方法类似,添加附加源S和附加汇T,从S向二分图X集合中每个顶点连接一条权值为0,容量为1的有向边,从Y集合中每个顶点向T也连接一条权值为0,容量为1的有向边。然后把原有的边变成容量为1,权值不变的有向边。求从S到T的最小(大)费用最大流,就能求得最小(大)权匹配。
上述建模求最大权匹配的方法求得的一定是最佳匹配(如果存在完备匹配),因为S到X集合每条边全部满流。如下图所示,最小费用最大流为2。
要求最大权匹配(不一定完备匹配)。如下图,只需再引入一个顶点A,从X集合的每个顶点向A连接一条容量为1,权值为0的边,然后再由A向T连接一条权值为0,容量不小于|X|的边,求最大费用最大流,这时是100。
最小权匹配也类似,不过新加的边权要为一个极大值,大于所有已有边权值。
[KM算法与费用流的比较]
从理论上分析,KM算法的时间复杂度比费用流要好,但是实际上和较好的费用流算法比起来运行效率是差不多的,KM算法优势仅仅在于编程容易。KM算法也有其不可避免的局限性,就是必须用邻接矩阵来表示。这样会浪费很多的空间,尤其是图相当稀疏的时候。而对于十分稀疏的图,许多优秀的费用流算法效率是很高的。这并不说明KM算法不如费用流,毕竟在信息学竞赛中,编程的复杂度也是一个相当重要的需要考虑的因素
先说KM算法求二分图的最佳匹配思想,再详讲KM的实现。
【KM算法求二分图的最佳匹配思想】
对于具有二部划分( V1, V2 )的加权完全二分图,其中 V1= { x1, x2, x3, … , xn }, V2= { y1, y2, y3, … , yn },边< xi, yj >具有权值 Wi,j 。该带权二分图中一个总权值最大的完美匹配,称之为最佳匹配。
记 L(x) 表示结点 x 的标记量,如果对于二部图中的任何边<x,y>,都有 L(x)+ L(y)>= Wx,y,我们称 L 为二部图的可行顶标。
设 G(V,E) 为二部图, G’(V,E’) 为二部图的子图。如果对于 G’ 中的任何边<x,y> 满足, L(x)+ L(y)== Wx,y,我们称 G’(V,E’) 为 G(V,E) 的等价子图。
定理一:设 L 是二部图 G 的可行顶标。若 L 等价子图 GL 有完美匹配 M,则 M 是 G 的最佳匹配。
证明:由于 GL 是 G 的等价子图,M 是 GL 的完美匹配,所以,M 也是 G 的完美匹配。以由于对于匹配 M 的每条边 e ,都有 e∈ E( GL ),而且 M 中每条边覆盖每个顶点正好一次,所以
W( M )= å W(e), e∈ M = å L(x), x∈ V
另一方面,对于 G 的任何完美匹配 M’ 有
W( M’ )= å W(e), e∈ M’ <= å L(x), x∈ V
于是 W( M )>= W( M’ ),即 M 是 G 的最优匹配。
由上述定理,我们可以通过来不断修改可行顶标,得到等价子图,从而求出最佳匹配。
就像匈牙利算法一样,我们依次为每一个顶点 i 寻找增广路径,如果寻找增广路径失败,我们就修改相应的可行顶标,来得到增广路径。
如图:
| 1 2 3 |
| 3 2 4 |
| 2 3 5 |
若要对这个完全二分图求最佳匹配
初始化:
Lx(1)= max{ y| w(1,y), 1<= y<= 3 }= max{ 1, 2, 3 }= 3, Ly(1)= 0
Lx(2)= max{ 3, 2, 4 }= 4, Ly(2)= 0
Lx(3)= max{ 2, 3, 5 }= 5, Ly(3)= 0;
我们建立等价子图( 满足 Lx(x)+ Ly(y)== W(x,y) ) 如下:
km算法求二分图最佳匹配
对于该图,运用匈牙利算法对 X 部顶点 1 求增广路径,得到一个匹配,如图( 红色代表匹配边 ):km算法求二分图最佳匹配
对 X 部顶点 2 求增广路径失败,寻找增广路径的过程为 X 2-> Y 3-> X 1。我们把寻找增广路径失败的 DFS 的交错树中,在 X 部顶点集称之为 S, 在 Y 部的顶点集称之为 T。则 S= { 1, 2 },T= { 3 }。现在我们就通过修改顶标值来扩大等价子图,如何修改。
1) 我们寻找一个 d 值,使得 d= min{ (x,y)| Lx(x)+ Ly(y)- W(x,y), x∈ S, y∉ T },因些,这时 d= min{
Lx(1)+Ly(1)-W(1,1), Lx(1)+Ly(2)-W(1,2), Lx(2)+Ly(1)-W(2,1), Lx(2)+Ly(2)-W(2,2) }=
min{ 3+0- 1, 3+0-2, 4+0-3, 4+0-2 }= min{ 2, 1, 1, 2 }= 1。
寻找最小的 d 是为了保证修改后仍满足性质对于边 <x,y> 有 Lx(x)+ Ly(y)>= W(x,y)。
2) 然后对于顶点 x
- 如果 x∈ S 则 Lx(x)= Lx(x)- d。
- 如果 x∈ T 则 Ly(x)= Ly(x)+ d。
- 其它情况保持不变。
如此修改后,我们发现对于边<x,y>,顶标 Lx(x)+ Ly(y) 的值为 - Lx(x)- d+ Ly(y)+ d, x∈ S, y∈ T。
- Lx(x)+ Ly(y), x∉ S, y∉ T。
- Lx(x)- d+ Ly(y), x∈ S, y∉ T。
- Lx(x)+ Ly(y)+ d, x∉ S, y∈ T。
易知,修改后对于任何边仍满足 Lx(x)+ Ly(y)>= W(x,y),并且第三种情况顶标值减少了 d,如此定会使等价子图扩大。
就上例而言: 修改后 Lx(1)= 2, Lx(2)= 3, Lx(3)= 5, Ly(1)= 0, Ly(1)= 0, Ly(2)= 0, Ly(3)= 1。
这时 Lx(2)+Ly(1)=3+0=3= W(2,1),在等价子图中增加了一条边,等价子图变为:
km算法求二分图最佳匹配
如此按以上方法,得到等价子图的完美匹配。
另外计算 d 值的时候可以进行一些优化。
定义 slack(y)= min{ (x,y)| Lx(x)+ Ly(y)- W(x,y),x∈ S, y∉ T }
这样能在寻找增广路径的时候就顺便将 slack 求出。
(以上为摘上网络)
【KM算法及其具体过程】
(1)可行点标:每个点有一个标号,记lx[i]为X方点i的标号,ly[j]为Y方点j的标号。如果对于图中的任意边(i, j, W)都有lx[i]+ly[j]>=W,则这一组点标是可行的。特别地,对于lx[i]+ly[j]=W的边(i, j, W),称为可行边;
(2)KM 算法的核心思想就是通过修改某些点的标号(但要满足点标始终是可行的),不断增加图中的可行边总数,直到图中存在仅由可行边组成的完全匹配为止,此时这个 匹配一定是最佳的(因为由可行点标的的定义,图中的任意一个完全匹配,其边权总和均不大于所有点的标号之和,而仅由可行边组成的完全匹配的边权总和等于所 有点的标号之和,故这个匹配是最佳的)。一开始,求出每个点的初始标号:lx[i]=max{e.W|e.x=i}(即每个X方点的初始标号为与这个X方 点相关联的权值最大的边的权值),ly[j]=0(即每个Y方点的初始标号为0)。这个初始点标显然是可行的,并且,与任意一个X方点关联的边中至少有一条可行边;
(3)然后,从每个X方点开始DFS增广。DFS增广的过程与最大匹配的Hungary算法基本相同,只是要注意两点:一是只找可行边,二是要把搜索过程中遍历到的X方点全部记下来(可以用vst搞一下),以进行后面的修改;
(4) 增广的结果有两种:若成功(找到了增广轨),则该点增广完成,进入下一个点的增广。若失败(没有找到增广轨),则需要改变一些点的标号,使得图中可行边的 数量增加。方法为:将所有在增广轨中(就是在增广过程中遍历到)的X方点的标号全部减去一个常数d,所有在增广轨中的Y方点的标号全部加上一个常数d,则 对于图中的任意一条边(i, j, W)(i为X方点,j为Y方点):
<1>i和j都在增广轨中:此时边(i, j)的(lx[i]+ly[j])值不变,也就是这条边的可行性不变(原来是可行边则现在仍是,原来不是则现在仍不是);
<2>i在增广轨中而j不在:此时边(i, j)的(lx[i]+ly[j])的值减少了d,也就是原来这条边不是可行边(否则j就会被遍历到了),而现在可能是;
<3>j在增广轨中而i不在:此时边(i, j)的(lx[i]+ly[j])的值增加了d,也就是原来这条边不是可行边(若这条边是可行边,则在遍历到j时会紧接着执行DFS(i),此时i就会被遍历到),现在仍不是;
<4>i和j都不在增广轨中:此时边(i, j)的(lx[i]+ly[j])值不变,也就是这条边的可行性不变。
这 样,在进行了这一步修改操作后,图中原来的可行边仍可行,而原来不可行的边现在则可能变为可行边。那么d的值应取多少?显然,整个点标不能失去可行性,也 就是对于上述的第<2>类边,其lx[i]+ly[j]>=W这一性质不能被改变,故取所有第<2>类边的 (lx[i]+ly[j]-W)的最小值作为d值即可。这样一方面可以保证点标的可行性,另一方面,经过这一步后,图中至少会增加一条可行边。
(5)修改后,继续对这个X方点DFS增广,若还失败则继续修改,直到成功为止;
(6)以上就是KM算法的基本思路。但是朴素的实现方法,时间复杂度为O(n4)——需要找O(n)次增广路,每次增广最多需要修改O(n)次顶标,每次修改顶 标时由于要枚举边来求d值,复杂度为O(n2)。实际上KM算法的复杂度是可以做到O(n3)的。我们给每个Y顶点一个“松弛量”函数slack,每次开 始找增广路时初始化为无穷大。在寻找增广路的过程中,检查边(i,j)时,如果它不在相等子图中,则让slack[j]变成原值与 A[i]+B[j]-w[i,j]的较小值。这样,在修改顶标时,取所有不在交错树中的Y顶点的slack值中的最小值作为d值即可。但还要注意一点:修 改顶标后,要把所有不在交错树中的Y顶点的slack值都减去d。
【求二分图的最小匹配】
只需把权值取反,变为负的,再用KM算出最大权匹配,取反则为其最小权匹配。
hdoj 2255
#include
#include
#define M 310
#define inf 0x3f3f3f3f
int n,nx,ny;
int link[M],lx[M],ly[M],slack[M]; //lx,ly为顶标,nx,ny分别为x点集y点集的个数
int visx[M],visy[M],w[M][M];
int DFS(int x)
{
visx[x] = 1;
for (int y = 1;y <= ny;y ++)
{
if (visy[y])
continue;
int t = lx[x] + ly[y] - w[x][y];
if (t == 0) //
{
visy[y] = 1;
if (link[y] == -1||DFS(link[y]))
{
link[y] = x;
return 1;
}
}
else if (slack[y] > t) //不在相等子图中slack 取最小的
slack[y] = t;
}
return 0;
}
int KM()
{
int i,j;
memset (link,-1,sizeof(link));
memset (ly,0,sizeof(ly));
for (i = 1;i <= nx;i ++) //lx初始化为与它关联边中最大的
for (j = 1,lx[i] = -inf;j <= ny;j ++)
if (w[i][j] > lx[i])
lx[i] = w[i][j];
for (int x = 1;x <= nx;x ++)
{
for (i = 1;i <= ny;i ++)
slack[i] = inf;
while (1)
{
memset (visx,0,sizeof(visx));
memset (visy,0,sizeof(visy));
if (DFS(x)) //若成功(找到了增广轨),则该点增广完成,进入下一个点的增广
break; //若失败(没有找到增广轨),则需要改变一些点的标号,使得图中可行边的数量增加。
//方法为:将所有在增广轨中(就是在增广过程中遍历到)的X方点的标号全部减去一个常数d,
//所有在增广轨中的Y方点的标号全部加上一个常数d
int d = inf;
for (i = 1;i <= ny;i ++)
if (!visy[i]&&d > slack[i])
d = slack[i];
for (i = 1;i <= nx;i ++)
if (visx[i])
lx[i] -= d;
for (i = 1;i <= ny;i ++) //修改顶标后,要把所有不在交错树中的Y顶点的slack值都减去d
if (visy[i])
ly[i] += d;
else
slack[i] -= d;
}
}
int res = 0;
for (i = 1;i <= ny;i ++)
if (link[i] > -1)
res += w[link[i]][i];
return res; } int main () {
int i,j;
while (scanf ("%d",&n)!=EOF)
{
nx = ny = n;
// memset (w,0,sizeof(w));
for (i = 1;i <= n;i ++)
for (j = 1;j <= n;j ++)
scanf ("%d",&w[i][j]);
int ans = KM();
printf ("%d\n",ans);
}
return 0; }
