信息熵

熵定义如下：
变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。香农不是用钱，而是用 “比特”（bit）这个概念来度量信息量。 信息量的比特数和所有可能情况的对数函数 log 有关。（二进制位数）常用的汉字（一级二级国标）大约有 7000 字。假如每个字等概率，那么我们大约需要 13 个比特（即 13 位二进制数）表示一个汉字。

信息量可以表示为：
-log2(pi)
即信息占的bit数
信息熵其实是一个随机变量信息量的数学期望。
H(X)=−∑P(x)logP(x))

信息熵（又叫香农熵 Shannon entropy）反映了一个系统的无序化（有序化）程度，一个系统越有序，信息熵就越低，反之就越高

相对熵（relative entropy）
所谓相对，自然在两个随机变量之间。又称互熵，Kullback–Leibler divergence（K-L 散度）等。设 p(x)和 q(x) 是 X取值的两个概率分布，则 p 对 q的相对熵为：
D(p||q)=∑i=1np(x)logp(x)q(x)

在一定程度上，熵可以度量两个随机变量的距离。KL 散度是两个概率分布 P 和 Q 差别的非对称性的度量。KL 散度是用来度量使用基于 Q 的编码来编码来自 P 的样本平均所需的额外的位元数。
典型情况下，P 表示数据的真实分布，Q 表示数据的理论分布，模型分布，或 P 的近似分布。
相对熵的性质，相对熵（KL散度）有两个主要的性质。如下
（1）尽管 KL 散度从直观上是个度量或距离函数，但它并不是一个真正的度量或者距离，因为它不具有对称性，即
D(p||q)≠D(q||p)
（2）相对熵的值为非负值，即
D(p||q)≥0

1. 交叉熵（cross entropy）
   H(p,q)=−∑xp(x)logq(x)
   在学习决策树时，最重要的步骤是构建决策树。

其中，最重要的步骤是根据属性划分数据集，其中先使用哪个属性，后使用哪个属性，是决定决策树构建的好坏的重要标准。

其中，使用属性构建数据集，最重要的参考标准，就是使划分后的信息增益最大。

熵：表示随机变量不确定性，即混乱程度的量化指标。

熵越大，不确定性越大，越无序；越小，确定性越大，越有序。

同理，一条信息的信息量大小，与不确定性直接相关。

不确定性越大，信息量越大，熵越大；

确定性越大，信息量越小，熵越小。

熵的单位是bit。

不计算信息量等，直接存储一个文件，需要的是正常的存储空间大小。

通过压缩算法，仅保留有用信息的情况下，存储的是文件的信息量。

两者数量上的差距，是冗余度。

由此可见：冗余度越大，可压缩的空间越大。反之，亦然。

另一种度量集合无序程度的方法是：Gini impurity，基尼不纯度。

信息增益
信息增益 = 信息熵 - 条件熵
信息增益代表了在一个条件下，信息复杂度（不确定性）减少的程度

条件熵

条件熵是用来解释信息增益而引入的概念，概率定义：随机变量X在给定条件下随机变量Y的条件熵，对定义描述为：X给定条件下Y的条件干率分布的熵对X的数学期望，在机器学习中为选定某个特征后的熵，公式如下：
H(Y|X)=∑p(x)H(Y|X=x)

3、信息增益
信息增益在决策树算法中是用来选择特征的指标，信息增益越大，则这个特征的选择性越好，在概率中定义为：待分类的集合的熵和选定某个特征的条件熵之差（这里只的是经验熵或经验条件熵，由于真正的熵并不知道，是根据样本计算出来的），公式如下：
IG=H(Y)-H(Y|X)

随机变量X（嫁与不嫁）的信息熵为：
嫁的个数为6个，占1/2，那么信息熵为-1/2log1/2-1/2log1/2 = -log1/2=0.301
现在假如我知道了一个男生的身高信息。身高有三个可能的取值{矮，中，高}
矮包括{1,2,3,5,6,11,12}，嫁的个数为1个，不嫁的个数为6个
中包括{8,9} ，嫁的个数为2个，不嫁的个数为0个
高包括{4,7,10}，嫁的个数为3个，不嫁的个数为0个

我们先求出公式对应的:
H(Y|X = 矮) = -1/7log1/7-6/7log6/7=0.178
H(Y|X=中) = -1log1-0 = 0
H(Y|X=高） = -1log1-0=0
p(X = 矮) = 7/12,p(X =中) = 2/12,p(X=高) = 3/12
则可以得出条件熵为：
7/120.178+2/120+3/12*0 = 0.103
那么我们知道信息熵与条件熵相减就是我们的信息增益，为0.301-0.103=0.198

信息增益是针对一个一个的特征而言的，就是看一个特征t，系统有它和没它的时候信息量各是多少，两者的差值就是这个特征给系统带来的信息量，即增益。系统含有特征t的时候信息量很好计算，就是刚才的式子，它表示的是包含所有特征时系统的信息量。

用决策树来预测：

决策树的形式类似于“如果天气怎么样，去玩；否则，怎么着怎么着”的树形分叉。那么问题是用哪个属性（即变量，如天气、温度、湿度和风力）最适合充当这颗树的根节点，在它上面没有其他节点，其他的属性都是它的后续节点。

那么借用上面所述的能够衡量一个属性区分以上数据样本的能力的“信息增益”（Information Gain）理论。

如果一个属性的信息增益量越大，这个属性作为一棵树的根节点就能使这棵树更简洁，比如说一棵树可以这么读成，如果风力弱，就去玩；风力强，再按天气、温度等分情况讨论，此时用风力作为这棵树的根节点就很有价值。如果说，风力弱，再又天气晴朗，就去玩；如果风力强，再又怎么怎么分情况讨论，这棵树相比就不够简洁了。

ID3使用信息增益，c4.5使用信息增益比来选择特征

作者：西门吹风
链接：https://www.zhihu.com/question/22928442/answer/117189907
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

而信息增益（Info-Gain）就是指划分前后信息熵的变化：在ID3算法中，信息增益（Info-Gain）越大，划分越好，决策树算法本质上就是要找出每一列的最佳划分以及不同列划分的先后顺序及排布。后面回到题中的问题，C4.5中使用信息增益率（Gain-ratio），ID3算法使用信息增益（Info-Gain），二者有何区别？根据前文的例子，Info-Gain在面对类别较少的离散数据时效果较好，上例中的outlook、temperature等数据都是离散数据，而且每个类别都有一定数量的样本，这种情况下使用ID3与C4.5的区别并不大。但如果面对连续的数据（如体重、身高、年龄、距离等），或者每列数据没有明显的类别之分（最极端的例子的该列所有数据都独一无二），在这种情况下，我们分析信息增益（Info-Gain）的效果：根据公式，E(S)为初始label列的熵，并未发生变化，则IGain(S,A)的大小取决于E(A)的大小，E(A)越小，IGain(S,A)越大，而根据前文例子，，若某一列数据没有重复，ID3算法倾向于把每个数据自成一类，此时，这样E(A)为最小，IGain(S,A)最大，程序会倾向于选择这种划分，这样划分效果极差。为了解决这个问题，引入了信息增益率（Gain-ratio）的概念，计算方式如下：，这里Info为划分行为带来的信息，信息增益率如下计算：这样就减轻了划分行为本身的影响。评论中很多人对文中信息量和熵的部分有疑问，这确实是个很绕的问题，
目前对于信息的定义主要有以下几种：香农（C. E. Shannon）信息是不确定性的消除维纳信息定义 信息是独立于物质、能量的一种属性标示。逆香农信息定义 信息是确定性的增加。邓宇等人的定义 信息是事物现象及其属性标识的集合。上面几种定义各不相同，答主比较倾向于逆香农信息定义，但本质上还是香农那一套。

基尼不纯度：将来自集合中的某种结果随机应用于集合中某一数据项的预期误差率。
公式：

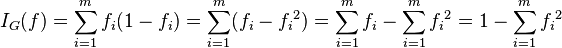
基尼不纯度的大概意思是 一个随机事件变成它的对立事件的概率
例如 一个随机事件X ，P(X=0) = 0.5 ,P(X=1)=0.5
那么基尼不纯度就为 P(X=0)(1 - P(X=0)) + P(X=1)(1 - P(X=1)) = 0.5

   一个随机事件Y ，P(Y=0) = 0.1 ,P(Y=1)=0.9

  那么基尼不纯度就为P(Y=0)*(1 - P(Y=0)) +   P(Y=1)*(1 - P(Y=1))  = 0.18

 很明显 X比Y更混乱，因为两个都为0.5 很难判断哪个发生。而Y就确定得多，Y=0发生的概率很大。而基尼不纯度也就越小。

所以基尼不纯度也可以作为 衡量系统混乱程度的 标准