一、一点历史

1976年以前，所有的加密方法都是同一种模式：

　　（1）甲方选择某一种加密规则，对信息进行加密；

　　（2）乙方使用同一种规则，对信息进行解密。

由于加密和解密使用同样规则（简称”密钥”），这被称为”对称加密算法”（Symmetric-key algorithm）。

这种加密模式有一个最大弱点：甲方必须把加密规则告诉乙方，否则无法解密。保存和传递密钥，就成了最头疼的问题。

1976年，两位美国计算机学家Whitfield Diffie 和 Martin Hellman，提出了一种崭新构思，可以在不直接传递密钥的情况下，完成解密。这被称为”Diffie-Hellman密钥交换算法”。这个算法启发了其他科学家。人们认识到，加密和解密可以使用不同的规则，只要这两种规则之间存在某种对应关系即可，这样就避免了直接传递密钥。

这种新的加密模式被称为”非对称加密算法”。
（1）乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的。
（2）甲方获取乙方的公钥，然后用它对信息加密。
（3）乙方得到加密后的信息，用私钥解密。

如果公钥加密的信息只有私钥解得开，那么只要私钥不泄漏，通信就是安全的。

1977年，三位数学家Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名，叫做RSA算法。从那时直到现在，RSA算法一直是最广为使用的”非对称加密算法”。毫不夸张地说，只要有计算机网络的地方，就有RSA算法。

这种算法非常可靠，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长RSA密钥是768个二进制位。也就是说，长度超过768位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024位的RSA密钥基本安全，2048位的密钥极其安全。

下面，我就进入正题，解释RSA算法的原理。文章共分成两部分，今天是第一部分，介绍要用到的四个数学概念。你可以看到，RSA算法并不难，只需要一点数论知识就可以理解。

二、互质关系

如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

关于互质关系，不难得到以下结论：

　　1. 任意两个质数构成互质关系，比如13和61。

1. 一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10。
   　　3. 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57。
   4. 1和任意一个自然数是都是互质关系，比如1和99。
   5. p是大于1的整数，则p和p-1构成互质关系，比如57和56。
   6. p是大于1的奇数，则p和p-2构成互质关系，比如17和15。

三、欧拉函数
请思考以下问题：
　　任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？（比如，在1到8之中，有多少个数与8构成互质关系？）

计算这个值的方法就叫做欧拉函数，以φ(n)表示。在1到8之中，与8形成互质关系的是1、3、5、7，所以 φ(n) = 4。

φ(n) 的计算方法并不复杂，但是为了得到最后那个公式，需要一步步讨论。

第一种情况

如果n=1，则 φ(1) = 1 。因为1与任何数（包括自身）都构成互质关系。

第二种情况

如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系。比如5与1、2、3、4都构成互质关系。

第三种情况

如果n是质数的某一个次方，即 n = p^k (p为质数，k为大于等于1的整数)，则

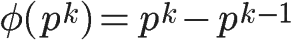
比如 φ(8) = φ(2^3) =2^3 - 2^2 = 8 -4 = 4。

这是因为只有当一个数不包含质数p，才可能与n互质。而包含质数p的数一共有p^(k-1)个，即1×p、2×p、3×p、…、p^(k-1)×p，把它们去除，剩下的就是与n互质的数。

上面的式子还可以写成下面的形式：

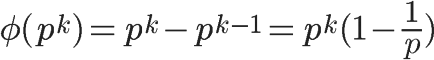
可以看出，上面的第二种情况是 k=1 时的特例。

第四种情况

如果n可以分解成两个互质的整数之积，

　　n = p1 × p2

则

　　φ(n) = φ(p1p2) = φ(p1)φ(p2)

即积的欧拉函数等于各个因子的欧拉函数之积。比如，φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24。

这一条的证明要用到”中国剩余定理”，这里就不展开了，只简单说一下思路：如果a与p1互质(a<p1)，b与p2互质(b<p2)，c与p1p2互质(c<p1p2)，则c与数对 (a,b) 是一一对应关系。由于a的值有φ(p1)种可能，b的值有φ(p2)种可能，则数对 (a,b) 有φ(p1)φ(p2)种可能，而c的值有φ(p1p2)种可能，所以φ(p1p2)就等于φ(p1)φ(p2)。
////////////
中国剩余定理
　　在《孙子算经》中有这样一个问题：“今有物不知其数，三三数之剩二（除以3余2），五五数之剩三（除以5余3），七七数之剩二（除以7余2），问物几何？”这个问题称为“孙子问题”，该问题的一般解法国际上称为“中国剩余定理”。具体解法分三步：

找出三个数：从3和5的公倍数中找出被7除余1的最小数15，从3和7的公倍数中找出被5除余1 的最小数21，最后从5和7的公倍数中找出除3余1的最小数70。
用15乘以2（2为最终结果除以7的余数），用21乘以3（3为最终结果除以5的余数），同理，用70乘以2（2为最终结果除以3的余数），然后把三个乘积相加15∗2+21∗3+70∗215∗2+21∗3+70∗2得到和233。
用233除以3，5，7三个数的最小公倍数105，得到余数23，即233%105=23233%105=23。这个余数23就是符合条件的最小数。
　　就这么简单。我们在感叹神奇的同时不禁想知道古人是如何想到这个方法的，有什么基本的数学依据吗？

　　我们将“孙子问题”拆分成几个简单的小问题，从零开始，试图揣测古人是如何推导出这个解法的。

　　首先，我们假设n1n1是满足除以3余2的一个数，比如2，5，8等等，也就是满足3∗k+2（k>=0）3∗k+2（k>=0）的一个任意数。同样，我们假设n2n2是满足除以5余3的一个数，n3n3是满足除以7余2的一个数。

　　有了前面的假设，我们先从n1n1这个角度出发，已知n1n1满足除以3余2，能不能使得n1+n2n1+n2的和仍然满足除以3余2？进而使得n1+n2+n3n1+n2+n3的和仍然满足除以3余2？

　　这就牵涉到一个最基本数学定理，如果有a%b=ca%b=c，则有(a+k∗b)%b=c(k为非零整数)(a+k∗b)%b=c(k为非零整数)，换句话说，如果一个除法运算的余数为cc，那么被除数与kk倍的除数相加（或相减）的和（差）再与除数相除，余数不变。这个是很好证明的。

　　以此定理为依据，如果n2n2是3的倍数，n1+n2n1+n2就依然满足除以3余2。同理，如果n3n3也是3的倍数，那么n1+n2+n3n1+n2+n3的和就满足除以3余2。这是从n1n1的角度考虑的，再从n2n2，n3n3的角度出发，我们可推导出以下三点：

为使n1+n2+n3n1+n2+n3的和满足除以3余2，n2n2和n3n3必须是3的倍数。
为使n1+n2+n3n1+n2+n3的和满足除以5余3，n1n1和n3n3必须是5的倍数。
为使n1+n2+n3n1+n2+n3的和满足除以7余2，n1n1和n2n2必须是7的倍数。
　　因此，为使n1+n2+n3n1+n2+n3的和作为“孙子问题”的一个最终解，需满足：

n1n1除以3余2，且是5和7的公倍数。
n2n2除以5余3，且是3和7的公倍数。
n3n3除以7余2，且是3和5的公倍数。
　　所以，孙子问题解法的本质是从5和7的公倍数中找一个除以3余2的数n1n1，从3和7的公倍数中找一个除以5余3的数n2n2，从3和5的公倍数中找一个除以7余2的数n3n3，再将三个数相加得到解。在求n1n1，n2n2，n3n3时又用了一个小技巧，以n1n1为例，并非从5和7的公倍数中直接找一个除以3余2的数，而是先找一个除以3余1的数，再乘以2。也就是先求出5和7的公倍数模3下的逆元，再用逆元去乘余数。

　　这里又有一个数学公式，如果a%b=ca%b=c，那么(a∗k)%b=a%b+a%b+…+a%b=c+c+…+c=k∗c(k>0)(a∗k)%b=a%b+a%b+…+a%b=c+c+…+c=k∗c(k>0),也就是说，如果一个除法的余数为cc，那么被除数的kk倍与除数相除的余数为k∗ck∗c。展开式中已证明。

　　最后，我们还要清楚一点，n1+n2+n3n1+n2+n3只是问题的一个解，并不是最小的解。如何得到最小解？我们只需要从中最大限度的减掉掉3，5，7的公倍数105即可。道理就是前面讲过的定理“如果a%b=ca%b=c，则有(a−k∗b)%b=c(a−k∗b)%b=c”。所以（n1+n2+n3）%105（n1+n2+n3）%105就是最终的最小解。

　　这样一来就得到了中国剩余定理的公式：

设正整数两两互素，则同余方程组
有整数解。并且在模下的解是唯一的，解为
其中，而为模的逆元。
////////////
第五种情况

因为任意一个大于1的正整数，都可以写成一系列质数的积。

根据第4条的结论，得到

再根据第3条的结论，得到

也就等于

这就是欧拉函数的通用计算公式。比如，1323的欧拉函数，计算过程如下：

四、欧拉定理

欧拉函数的用处，在于欧拉定理。”欧拉定理”指的是：

如果两个正整数a和n互质，则n的欧拉函数 φ(n) 可以让下面的等式成立：

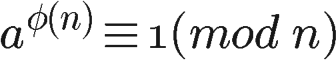
也就是说，a的φ(n)次方被n除的余数为1。或者说，a的φ(n)次方减去1，可以被n整除。比如，3和7互质，而7的欧拉函数φ(7)等于6，所以3的6次方（729）减去1，可以被7整除（728/7=104）。

欧拉定理的证明比较复杂，这里就省略了。我们只要记住它的结论就行了。

欧拉定理可以大大简化某些运算。比如，7和10互质，根据欧拉定理，

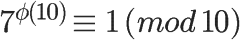
已知 φ(10) 等于4，所以马上得到7的4倍数次方的个位数肯定是1。

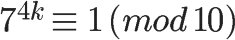
因此，7的任意次方的个位数（例如7的222次方），心算就可以算出来。

欧拉定理有一个特殊情况。

假设正整数a与质数p互质，因为质数p的φ(p)等于p-1，则欧拉定理可以写成

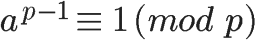
这就是著名的费马小定理。它是欧拉定理的特例。

欧拉定理是RSA算法的核心。理解了这个定理，就可以理解RSA。

五、模反元素

还剩下最后一个概念：

如果两个正整数a和n互质，那么一定可以找到整数b，使得 ab-1 被n整除，或者说ab被n除的余数是1。

ab三1(mod n)

这时，b就叫做a的”模反元素”。

比如，3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 {…,-18,-7,4,15,26,…}，即如果b是a的模反元素，则 b+kn 都是a的模反元素。

欧拉定理可以用来证明模反元素必然存在。

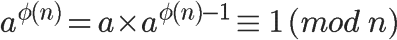
可以看到，a的 φ(n)-1 次方，就是a的模反元素。

==========================================
六、密钥生成的步骤

我们通过一个例子，来理解RSA算法。假设爱丽丝要与鲍勃进行加密通信，她该怎么生成公钥和私钥呢？

第一步，随机选择两个不相等的质数p和q。

爱丽丝选择了61和53。（实际应用中，这两个质数越大，就越难破解。）

第二步，计算p和q的乘积n。

爱丽丝就把61和53相乘。

　　n = 61×53 = 3233

n的长度就是密钥长度。3233写成二进制是110010100001，一共有12位，所以这个密钥就是12位。实际应用中，RSA密钥一般是1024位，重要场合则为2048位。

第三步，计算n的欧拉函数φ(n)。

根据公式：

　　φ(n) = (p-1)(q-1)

爱丽丝算出φ(3233)等于60×52，即3120。

第四步，随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质。

爱丽丝就在1到3120之间，随机选择了17。（实际应用中，常常选择65537。）

第五步，计算e对于φ(n)的模反元素d。

所谓”模反元素”就是指有一个整数d，可以使得ed被φ(n)除的余数为1。

　　ed ≡ 1 (mod φ(n))

这个式子等价于

　　ed - 1 = kφ(n)

于是，找到模反元素d，实质上就是对下面这个二元一次方程求解。

　　ex + φ(n)y = 1

已知 e=17, φ(n)=3120，

　　17x + 3120y = 1

这个方程可以用”扩展欧几里得算法”求解，此处省略具体过程。总之，爱丽丝算出一组整数解为 (x,y)=(2753,-15)，即 d=2753。

至此所有计算完成。

第六步，将n和e封装成公钥，n和d封装成私钥。

在爱丽丝的例子中，n=3233，e=17，d=2753，所以公钥就是 (3233,17)，私钥就是（3233, 2753）。

实际应用中，公钥和私钥的数据都采用ASN.1格式表达（实例）。

七、RSA算法的可靠性

回顾上面的密钥生成步骤，一共出现六个数字：

　　p
　　q
　　n
　　φ(n)
　　e
　　d

这六个数字之中，公钥用到了两个（n和e），其余四个数字都是不公开的。其中最关键的是d，因为n和d组成了私钥，一旦d泄漏，就等于私钥泄漏。

那么，有无可能在已知n和e的情况下，推导出d？

　　（1）ed≡1 (mod φ(n))。只有知道e和φ(n)，才能算出d。

　　（2）φ(n)=(p-1)(q-1)。只有知道p和q，才能算出φ(n)。

　　（3）n=pq。只有将n因数分解，才能算出p和q。

结论：如果n可以被因数分解，d就可以算出，也就意味着私钥被破解。

可是，大整数的因数分解，是一件非常困难的事情。目前，除了暴力破解，还没有发现别的有效方法。维基百科这样写道：

　　”对极大整数做因数分解的难度决定了RSA算法的可靠性。换言之，对一极大整数做因数分解愈困难，RSA算法愈可靠。

　　假如有人找到一种快速因数分解的算法，那么RSA的可靠性就会极度下降。但找到这样的算法的可能性是非常小的。今天只有短的RSA密钥才可能被暴力破解。到2008年为止，世界上还没有任何可靠的攻击RSA算法的方式。

　　只要密钥长度足够长，用RSA加密的信息实际上是不能被解破的。”

举例来说，你可以对3233进行因数分解（61×53），但是你没法对下面这个整数进行因数分解。

　　12301866845301177551304949
　　58384962720772853569595334
　　79219732245215172640050726
　　36575187452021997864693899
　　56474942774063845925192557
　　32630345373154826850791702
　　61221429134616704292143116
　　02221240479274737794080665
　　351419597459856902143413

它等于这样两个质数的乘积：

　　33478071698956898786044169
　　84821269081770479498371376
　　85689124313889828837938780
　　02287614711652531743087737
　　814467999489
　　　　×
　　36746043666799590428244633
　　79962795263227915816434308
　　76426760322838157396665112
　　79233373417143396810270092
　　798736308917

事实上，这大概是人类已经分解的最大整数（232个十进制位，768个二进制位）。比它更大的因数分解，还没有被报道过，因此目前被破解的最长RSA密钥就是768位。

八、加密和解密

有了公钥和密钥，就能进行加密和解密了。

（1）加密要用公钥 (n,e)

假设鲍勃要向爱丽丝发送加密信息m，他就要用爱丽丝的公钥 (n,e) 对m进行加密。这里需要注意，m必须是整数（字符串可以取ascii值或unicode值），且m必须小于n。

所谓”加密”，就是算出下式的c：

　　me ≡ c (mod n)

爱丽丝的公钥是 (3233, 17)，鲍勃的m假设是65，那么可以算出下面的等式：

　　6517 ≡ 2790 (mod 3233)

于是，c等于2790，鲍勃就把2790发给了爱丽丝。

（2）解密要用私钥(n,d)

爱丽丝拿到鲍勃发来的2790以后，就用自己的私钥(3233, 2753) 进行解密。可以证明，下面的等式一定成立：

　　cd ≡ m (mod n)

也就是说，c的d次方除以n的余数为m。现在，c等于2790，私钥是(3233, 2753)，那么，爱丽丝算出

　　27902753 ≡ 65 (mod 3233)

因此，爱丽丝知道了鲍勃加密前的原文就是65。

至此，”加密–解密”的整个过程全部完成。

我们可以看到，如果不知道d，就没有办法从c求出m。而前面已经说过，要知道d就必须分解n，这是极难做到的，所以RSA算法保证了通信安全。

你可能会问，公钥(n,e) 只能加密小于n的整数m，那么如果要加密大于n的整数，该怎么办？有两种解决方法：一种是把长信息分割成若干段短消息，每段分别加密；另一种是先选择一种”对称性加密算法”（比如DES），用这种算法的密钥加密信息，再用RSA公钥加密DES密钥。

九、私钥解密的证明

最后，我们来证明，为什么用私钥解密，一定可以正确地得到m。也就是证明下面这个式子：

　　cd ≡ m (mod n)

因为，根据加密规则

　　ｍe ≡ c (mod n)

于是，c可以写成下面的形式：

　　c = me - kn

将c代入要我们要证明的那个解密规则：

　　(me - kn)d ≡ m (mod n)

它等同于求证

　　med ≡ m (mod n)

由于

　　ed ≡ 1 (mod φ(n))

所以

　　ed = hφ(n)+1

将ed代入：

　　mhφ(n)+1 ≡ m (mod n)

接下来，分成两种情况证明上面这个式子。

（1）m与n互质。

根据欧拉定理，此时

　　mφ(n) ≡ 1 (mod n)

得到

　　(mφ(n))h × m ≡ m (mod n)

原式得到证明。

（2）m与n不是互质关系。

此时，由于n等于质数p和q的乘积，所以m必然等于kp或kq。

以 m = kp为例，考虑到这时k与q必然互质，则根据欧拉定理，下面的式子成立：

　　(kp)q-1 ≡ 1 (mod q)

进一步得到

　　[(kp)q-1]h(p-1) × kp ≡ kp (mod q)

即

　　(kp)ed ≡ kp (mod q)

将它改写成下面的等式

　　(kp)ed = tq + kp

这时t必然能被p整除，即 t=t’p

　　(kp)ed = t’pq + kp

因为 m=kp，n=pq，所以

　　med ≡ m (mod n)

原式得到证明。